
����Ŀ��ij��ѧ��ʦ�ڼס�������ƽ�а���á���ͳ��ѧ���͡���Ч���á����ֲ�ͬ�Ľ�ѧģʽ���н�ѧʵ��.Ϊ�˽�̸�ʵЧ�����п��Ժֱ���������и������ȡ![]() ��ѧ������ѧ�ɼ�����ͳ�ƣ��õ����µľ�Ҷͼ��
��ѧ������ѧ�ɼ�����ͳ�ƣ��õ����µľ�Ҷͼ��
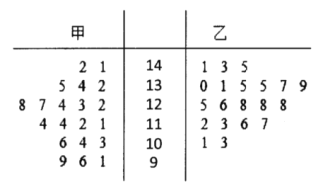
������ס��������ȡ�ķ�������λ���������Ƽס���������ѧ��ƽ��ˮƽ�ͷ�ɢ�̶ȣ���Ҫ����������ֵ���������ۼ��ɣ���
�������涨������![]() ��Ϊ���ã����ѴӼס�������ɼ�Ϊ���õ�ͬѧ�У��÷ֲ���������
��Ϊ���ã����ѴӼס�������ɼ�Ϊ���õ�ͬѧ�У��÷ֲ���������![]() λͬѧ�����ʾ����飬����
λͬѧ�����ʾ����飬����![]() λͬѧ��ǡ���ס�����������
λͬѧ��ǡ���ס�����������![]() �����ϵ�ͬѧ�ĸ���.
�����ϵ�ͬѧ�ĸ���.
���𰸡�����118��128��������������![]() .
.
��������
��������λ���ĸ���ɵó���λ��ֵ���ɾ�Ҷͼ�������ҵ�ƽ��ˮƽ�ͷ�ɢ�̶ȣ����Է������ɣ�
�����ɷֲ�����ĸ���ɵ�Ӧ�Ӽס�����������![]() �ˡ�
�ˡ�![]() �ˣ�����������Ͻ��������¼�ͬʱ�����ĸ��ʹ�ʽȷ�������ʼ���.
�ˣ�����������Ͻ��������¼�ͬʱ�����ĸ��ʹ�ʽȷ�������ʼ���.
�����ݾ�Ҷͼ�ã�
�װ���ͬѧ��������λ����![]() ��
��
�Ұ���ͬѧ��������λ����![]() .
.
�Ұ�ѧ����ѧ���Է�����ƽ��ˮƽ���ڼװ�ѧ����ѧ���Է�����ƽ��ˮƽ��
�װ�ѧ����ѧ���Է����ķ�ɢ�̶ȸ����Ұ�ѧ����ѧ���Է����ķ�ɢ�̶�.
�����ݾ�Ҷͼ��֪��
�ס���������ѧ�ɼ�Ϊ����������ֱ�Ϊ![]() ��
��![]() ������
������![]() �����ϵ���2�ˣ�3�ˣ�
�����ϵ���2�ˣ�3�ˣ�
���÷ֲ���������![]() �ˣ���Ӧ�Ӽס�����������
�ˣ���Ӧ�Ӽס�����������![]() �ˡ�
�ˡ�![]() ��.
��.
�衰�����![]() ����ǡ���мס������������
����ǡ���мס������������![]() �����ϵ�ͬѧ��Ϊ�¼�
�����ϵ�ͬѧ��Ϊ�¼�![]() ��
��
��![]() .
.
�ʣ������![]() ����ǡ���мס������������
����ǡ���мס������������![]() �����ϵ�ͬѧ�ĸ���Ϊ
�����ϵ�ͬѧ�ĸ���Ϊ![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���人���ֵ�����״������һ�ֿ���ͨ����ĭ�����ı��첡����ijҩ���о���Ϊɸ�������״��������Ҫ����ѪҺ�Ƿ�Ϊ���ԣ�����![]() ��ѪҺ������ÿ������ȡ���Ŀ����Ծ��ȣ����������ּ��鷽ʽ������ݼ��飬����Ҫ����n�Σ��ڻ�ϼ��飬������
��ѪҺ������ÿ������ȡ���Ŀ����Ծ��ȣ����������ּ��鷽ʽ������ݼ��飬����Ҫ����n�Σ��ڻ�ϼ��飬������![]() ��ѪҺ�����ֱ�ȡ�������һ�����.��������Ϊ���ԣ���k��ѪҺȫΪ���ԣ������k��ѪҺ��������һ�ξ��ˣ����������Ϊ���ԣ�Ϊ����ȷ��k��ѪҺ�����ļ���Ϊ���ԣ���Ҫ����k��ѪҺ����ݼ��飬��ʱ��k��ѪҺ�ļ�������ܹ�Ϊ
��ѪҺ�����ֱ�ȡ�������һ�����.��������Ϊ���ԣ���k��ѪҺȫΪ���ԣ������k��ѪҺ��������һ�ξ��ˣ����������Ϊ���ԣ�Ϊ����ȷ��k��ѪҺ�����ļ���Ϊ���ԣ���Ҫ����k��ѪҺ����ݼ��飬��ʱ��k��ѪҺ�ļ�������ܹ�Ϊ![]() ��.�����ڽ��ܼ����ѪҺ�����У�ÿ�������ļ����������Ի������Զ��Ƕ����ģ���ÿ�����������Խ���ĸ���Ϊ
��.�����ڽ��ܼ����ѪҺ�����У�ÿ�������ļ����������Ի������Զ��Ƕ����ģ���ÿ�����������Խ���ĸ���Ϊ![]() .
.
��1��������5��ѪҺ����������ֻ��2��Ϊ���ԣ�����ȡ��ݼ��鷽ʽ����ǡ�þ���2�μ�����ܰ���������ȫ����������ĸ��ʣ�
��2����ȡ����![]() ��ѪҺ�������Dz�����ݼ��鷽ʽ��������Ҫ����Ĵ���Ϊ
��ѪҺ�������Dz�����ݼ��鷽ʽ��������Ҫ����Ĵ���Ϊ![]() �����û�ϼ��鷽ʽ��������Ҫ������ܴ���Ϊ
�����û�ϼ��鷽ʽ��������Ҫ������ܴ���Ϊ![]() .
.
��i�������ø���ͳ��֪ʶ����![]() ������P����k�ĺ�����ϵʽ
������P����k�ĺ�����ϵʽ![]() ��
��
��ii����![]() �����û�ϼ��鷽ʽ����ʹ����k��ѪҺ������Ҫ������ܴ���������ֵ����ݼ�����ܴ�������ֵ���٣���k�����ֵ.
�����û�ϼ��鷽ʽ����ʹ����k��ѪҺ������Ҫ������ܴ���������ֵ����ݼ�����ܴ�������ֵ���٣���k�����ֵ.
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
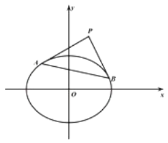
����Ŀ������Բ![]() ��һ��
��һ��![]() ����Բ
����Բ![]() ������
������![]() ��
��![]() ���е�ֱ�Ϊ
���е�ֱ�Ϊ![]() ��
��![]() ������
������![]() .
.
��1����![]() �Ĺ켣����
�Ĺ켣����
��2����![]() �����(��
�����(��![]() �����
�ĺ�����![]() ��ʾ)
��ʾ)
��3����![]() �˶�ʱ����
�˶�ʱ����![]() �����ȡֵ��Χ.
�����ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����Acos����x+������A��0������0��0������������ͼ���һ����ߵ�Ϊ��![]() ������֮���ڵ�һ���Գ�����Ϊ
������֮���ڵ�һ���Գ�����Ϊ![]() ����f��x����ͼ������ƽ��
����f��x����ͼ������ƽ��![]() ����λ���ȵõ�����g��x����ͼ���� ��
����λ���ȵõ�����g��x����ͼ���� ��
A.g��x��Ϊż����
B.g��x����һ��������������Ϊ![]()
C.g��x��Ϊ�溯��
D.����g��x����![]() �����������
�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C1��![]() ��ԲC2��(x-6)2+(y-1)2=1����ԲC2��һ��P��Բ������MN��������C����M��N���㣬����PΪMN���е㣬������MN��б��k>1ʱ��ֱ�߷���Ϊ�� ��
��ԲC2��(x-6)2+(y-1)2=1����ԲC2��һ��P��Բ������MN��������C����M��N���㣬����PΪMN���е㣬������MN��б��k>1ʱ��ֱ�߷���Ϊ�� ��
A.4x-3y-22=0B.4x-3y-16=0C.2x-y-11+5=0D.4x-3y-26=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2��2x������E��a��0����ֱ��l��C���ڲ�ͬ������P��x1��y1����Q��x2��y2����������y1y2����4����QΪ�е���߶ε����˵�ֱ�ΪM��N������N��x���ϣ�M��C�ϣ���a��_____��|PM|����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�����C�IJ�������Ϊ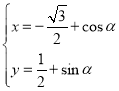 ��
��![]() Ϊ��������������ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ��
Ϊ��������������ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ��
��1��������l�ļ����귽��Ϊ![]() ��������l������C����A��B���㣬��AB�ij���
��������l������C����A��B���㣬��AB�ij���
��2����M��N������C�ϵ����㣬����MON![]() ����
����![]() ����������ֵ��
����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�س����˳溦��ũҵ��ѧ�����������溦ָ��������![]() ��
��![]() ��ʾ��
��ʾ��![]() �ܵij溦�����س̶ȣ��溦ָ��Խ�����س̶�Խ�ߣ�Ϊ�������溦����Ҫ�������Ρ�ɱ�棬Ȼ������������Դ���ޣ�ÿ��ֻ�ܲ�ȡ������������֮һ��
�ܵij溦�����س̶ȣ��溦ָ��Խ�����س̶�Խ�ߣ�Ϊ�������溦����Ҫ�������Ρ�ɱ�棬Ȼ������������Դ���ޣ�ÿ��ֻ�ܲ�ȡ������������֮һ��
����![]() ���������Σ����溦ָ������������
���������Σ����溦ָ������������![]() ��
��
����![]() ��ɱ�棬���溦ָ������������
��ɱ�棬���溦ָ������������![]() ��
��
��ij�����溦ָ����С��1ʱ��Σ���������ܽ��.
��1�����һ�ܵij溦ָ��![]() ������һ�����Խ�ʹ�ڶ��ܵij溦���س̶ȸ�С��
������һ�����Խ�ʹ�ڶ��ܵij溦���س̶ȸ�С��
��2�����һ�ܵij溦ָ��![]() �����ÿ�ܶ��������ŵIJ��ԣ��溦��Σ������ڵڼ��ܽ����
�����ÿ�ܶ��������ŵIJ��ԣ��溦��Σ������ڵڼ��ܽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
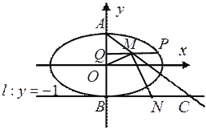
����Ŀ����ͼ����֪������ԭ�㣬������![]() ���ϵ���Բ��һ������Ϊ
���ϵ���Բ��һ������Ϊ![]() ��
�� 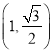 ����Բ�ϵ�һ���㣮
����Բ�ϵ�һ���㣮
��1������Բ�ı����̣�
��2������Բ���ϡ��¶���ֱ�Ϊ![]() ��
�� ![]() ��
��![]() ������Բ������
������Բ������![]() ������һ�㣬
������һ�㣬 ![]() �ᣬ
�ᣬ ![]() Ϊ���㣬
Ϊ���㣬 ![]() Ϊ�߶�
Ϊ�߶�![]() �е㣬ֱ��
�е㣬ֱ��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ,
, ![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬���
���е㣬���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com