练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某同学用收集到的6组数据对制作成如图所示的散点图（点旁的数据为该点坐标），并由最小二乘法计算得到回归直线的方程：，相关系数为，相关指数为；经过残差分析确定点为“离群点”（对应残差过大的点），把它去掉后，再用剩下的5组数据计算得到回归直线的方程：，相关系数为，相关指数为.则以下结论中，不正确的是（ ）

    A. ， B. ，

    C. D.

    【答案】D

    【解析】分析：利用回归方程的性质，利用相关系数和相关指数分析解答.

    详解：从图形中可以看出，两个变量是正相关，所以选项A是正确的；从图形中可以看出，回归直线的纵截距是正数，所以选项B和C是正确的；因为其中=真实值-预报值=残差，值越大，说明残差的平方和越小，也就是说模型的拟合效果越好.所以选项D是错误的.故答案为：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某地区上年度电价为元/kWh，年用电量为kWh．本年度计划将电价降低到0．55元/ kWh到0．75元/ kWh之间，而用户期望电价为0．40元/ kWh．经测算，下调电价后新增用电量与实际电价与用户的期望电价的差成反比（比例系数为），该地区电力的成本价为0．30元/ kWh．

    （1）写出本年度电价下调后，电力部门的收益与实际电价之间的函数关系式；

    （2）设=，当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%？（注：收益=实际电量×（实际电价-成本价））

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国南宋时期的著名数学家秦九韶在他的著作《数学九章》中提出了秦九韶算法来计算多项式的值，在执行如图算法的程序框图时，若输入的n=5，x=2，则输出V的值为（ ）
    A.15
    B.31
    C.63
    D.127

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某教师调查了名高三学生购买的数学课外辅导书的数量，将统计数据制成如下表格：

    男生

    女生

    总计

    购买数学课外辅导书超过本

    购买数学课外辅导书不超过本

    总计

    （Ⅰ）根据表格中的数据，是否有的把握认为购买数学课外辅导书的数量与性别相关；

    （Ⅱ）从购买数学课外辅导书不超过本的学生中，按照性别分层抽样抽取人，再从这人中随机抽取人询问购买原因，求恰有名男生被抽到的概率.

    附： ， .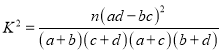

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f(x)=logax(a>0且a≠1)的图象过点(4,2),

    (1)求a的值.

    (2)若g(x)=f(1-x)+f(1+x),求g(x)的解析式及定义域.

    (3)在(2)的条件下,求g(x)的单调减区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校在本校任选了一个班级，对全班50名学生进行了作业量的调查，根据调查结果统计后，得到如下的列联表，已知在这50人中随机抽取1人，认为作业量大的概率为.

    认为作业量大

    认为作业量不大

    合计

    男生

    18

    女生

    17

    合计

    50

    （Ⅰ）请完成上面的列联表；

    （Ⅱ）根据列联表的数据，能否有的把握认为“认为作业量大”与“性别”有关？

    附表：

    0.100

    0.050

    0.025

    0.010

    0.001

    2.706

    3.841

    span>5.024

    6.635

    10.828

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合A={x|x2-3x+2=0}，B={x|x2+（a-1）x+a2-5=0}．

    （1）若A∩B={2}，求实数a的值；

    （2）若A∪B=A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，则下列结论正确的是（ ）

    A.当时，函数在上有最小值；

    B.当时，函数在上有最小值；

    C.对任意的实数，函数的图象关于点对称；

    D.方程可能有三个实数根.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥的底面是正方形，底面.

    （1）求证：直线平面；

    （2）当的值为多少时，二面角的大小为？

    查看答案和解析>>

    同步练习册答案