
【题目】当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() .
.
【答案】详见解析
【解析】
试题分析:本题考查含参数一元二次不等式问题,由于![]() ,所以方程
,所以方程![]() 的两个实根分别为
的两个实根分别为![]() ,分三种情况进行讨论,当
,分三种情况进行讨论,当![]() ,即
,即![]() 时,结合相应函数图象可知,不等式的解集为
时,结合相应函数图象可知,不等式的解集为![]() ,当
,当![]() ,即
,即![]() 时,结合相应函数图象可知,不等式的解集为
时,结合相应函数图象可知,不等式的解集为![]() ,当
,当![]() ,即
,即![]() 时,结合相应函数图象可知,不等式的解集为
时,结合相应函数图象可知,不等式的解集为![]() ,本题主要考查分类讨论思想方法、考查数形结合思想方法,需要注意的是在对参数讨论时,要做到“不重不漏”,考查学生基本运算能力,属于常规考查.
,本题主要考查分类讨论思想方法、考查数形结合思想方法,需要注意的是在对参数讨论时,要做到“不重不漏”,考查学生基本运算能力,属于常规考查.
试题解析:由于a>0,所以原不等式可化为(x-2)(x-![]() )>0,
)>0,
由![]() =2可得a=1,
=2可得a=1,
当0<a<1时,解不等式可得x<2或x>![]() ;
;
当a=1时,解不等式得x∈R且x≠2;
当a>1时,解不等式得x<![]() 或x>2.
或x>2.
综上所述,当0<a<1时,原不等式的解集为{x|x>![]() 或x<2},
或x<2},
当a=1时,原不等式的解集为{x|x≠2},
当a>1时,原不等式的解集为{x|x>2或x<![]() }
}


科目:高中数学 来源: 题型:
【题目】一个人连续射击三次,事件“至少有一次击中目标”的对立事件是( )
A.至多有一次击中目标B.三次都击不中目标
C.三次都击中目标D.只有一次击中目标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.

(1)证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的方程;
(2)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() 的面积;
的面积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?若存在,求出
为邻边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我国各景点在大众中的熟知度,随机对![]() ~
~![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组[ | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
![]()
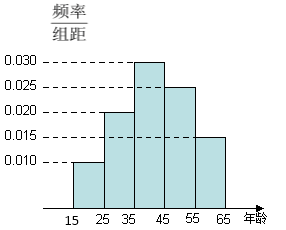
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组各抽取多少人;
组每组各抽取多少人;
(3)在(2)的条件下抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求所抽取的人中恰好没有第
人,求所抽取的人中恰好没有第![]() 组人的概率.
组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
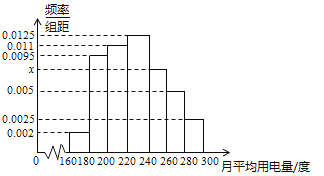
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为3的正三角形![]() 中,
中,![]() 分别是
分别是![]() 边上的点,满足
边上的点,满足![]() (如图
(如图![]() ),将
),将![]() 折起到
折起到![]() 的位置上,连接
的位置上,连接![]() (如图).
(如图).
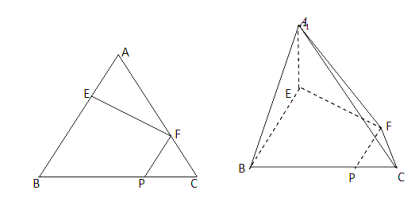
(1)在线段A1C上是否存在点Q,使得面QFP//面A1EB,证明你的结论;
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110,且a1,a2,a4成等比数列。
(1)证明:a1=d;
(2)求公差d的值和数列{an}的通项公式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com