
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为![]() 的样本,测量树苗高度(单位:
的样本,测量树苗高度(单位:![]() ),经统计,其高度均在区间
),经统计,其高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成
分成![]() 组,制成如图所示的频率分布直方图.其中高度为27cm及以上的树苗为优质树苗.
组,制成如图所示的频率分布直方图.其中高度为27cm及以上的树苗为优质树苗.


(1)求图中![]() 的值;
的值;
(2)已知所抽取这![]() 棵树苗来自于
棵树苗来自于![]() 两个试验区,部分数据如下列联表:将列联表补充完整,并判断是否有
两个试验区,部分数据如下列联表:将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: ,其中
,其中![]() .
.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n。如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
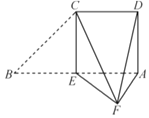
【题目】如图,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AB的中点
,E为AB的中点![]() 将
将![]() 沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为
沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为![]() .
.
![]() 求证:平面
求证:平面![]() 平面AEF;
平面AEF;
![]() 求直线DF与平面CEF所成角的正弦值.
求直线DF与平面CEF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com