
【题目】定义运算“![]() ”:对于任意
”:对于任意![]() ,
,![]() (等式的右边是通常的加减乘运算).若数列
(等式的右边是通常的加减乘运算).若数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() 对任意
对任意![]() 都成立.
都成立.
(1)求![]() 的值,并推导出用
的值,并推导出用![]() 表示
表示![]() 的解析式;
的解析式;
(2)若![]() ,令
,令![]() ,证明数列
,证明数列![]() 是等差数列;
是等差数列;
(3)若![]() ,令
,令![]() ,数列
,数列![]() 满足
满足![]() ,求正实数b的取值范围.
,求正实数b的取值范围.
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)直接利用信息的应用和赋值法的应用求出函数的关系式的表达式;
(2)利用构造法对和数列的关系式进行变换,进一步利用定义求出数列的通项公式;
(3)利用(1)和(2)的结论,进一步函数的单调性和极限的应用求出参数的取值范围.
(1)∵![]() ,
,![]() .
.
令![]() ,得
,得![]() ,
,![]() .
.
当![]() 时,有
时,有![]() .
.![]() ,
,
![]() .
.
(2)![]() ,
,![]() ,整理得
,整理得![]() .
.![]() .
.
∴数列![]() 是以首项为1、公差为
是以首项为1、公差为![]() 的等差数列.
的等差数列.
(3)结合(1),且![]() ,
,![]() ,即
,即![]() .
.![]() .
.
当![]() 时,
时,![]() ,此时,
,此时,![]() ,总是满足
,总是满足![]() ;
;
当![]() 时,
时,![]() ,此时,
,此时,![]() 是等比数列.
是等比数列.![]() .
.![]() .
.
若![]() 时,数列
时,数列![]() 是单调递增数列,且
是单调递增数列,且![]() 时,
时,![]() ,不满足
,不满足![]() .
.
若![]() 时,
时,![]() , 数列
, 数列![]() 是单调递减数列,故
是单调递减数列,故![]() 又
又![]() ,同样恒有
,同样恒有![]() 成立;
成立;
若![]() 时,
时,![]() ,数列
,数列![]() 是单调递增数列,
是单调递增数列,![]() .
.
由![]() ,即此时当
,即此时当![]() 时,满足
时,满足![]() .
.
综上,所求实数![]() 的取值范围是
的取值范围是![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】某校象棋社团组织中国象棋比赛,采用单循环赛制,即要求每个参赛选手必须且只须和其他选手各比赛一场,胜者得![]() 分,负者得
分,负者得![]() 分,平局两人各得
分,平局两人各得![]() 分.若冠军获得者得分比其他人都多,且获胜场次比其他人都少,则本次比赛的参赛人数至少为
分.若冠军获得者得分比其他人都多,且获胜场次比其他人都少,则本次比赛的参赛人数至少为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 是函数
是函数![]() 的一个极值点,试求
的一个极值点,试求![]() 的单调区间;
的单调区间;
(2)若![]() 且
且![]() ,是否存在实数a,使得
,是否存在实数a,使得![]() 在区间
在区间![]() 上的最大值为4?若存在,求出实数a的值;若不存在,请说明理由.
上的最大值为4?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
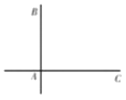
【题目】如图,两铁路线垂直相交于站![]() ,若已知
,若已知![]() 千米,甲火车从
千米,甲火车从![]() 站出发,沿
站出发,沿![]() 方向以
方向以![]() 千米
千米![]() 小时的速度行驶,同时乙火车从
小时的速度行驶,同时乙火车从![]() 站出发,沿
站出发,沿![]() 方向,以
方向,以![]() 千米
千米![]() 小时的速度行驶,至
小时的速度行驶,至![]() 站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
(1)求甲、乙两车的最近距离(用含![]() 的式子表示);
的式子表示);
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为![]() 小时,问
小时,问![]() 为何值时
为何值时![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年3月5日,国务院总理李克强作出的政府工作报告中,提到要“惩戒学术不端,力戒学术不端,力戒浮躁之风”.教育部2014年印发的《学术论文抽检办法》通知中规定:每篇抽检的学术论文送3位同行专家进行评议,3位专家中有2位以上(含3位)专家评议意见为“不合格”的学术论文,将认定为“存在问题学术论文”.有且只有1位专家评议意见为“不合格”的学术论文,将再送另外2位同行专家(不同于前3位专家)进行复评,2位复评专家中有1位以上(含1位)专家评议意见为“不合格”的学术论文,将认定为“存在问题学术论文”.设每篇学术论文被每位专家评议为“不合格”的概率均为![]() ,且各篇学术论文是否被评议为“不合格”相互独立.
,且各篇学术论文是否被评议为“不合格”相互独立.
(1)若![]() ,求抽检一篇学术论文,被认定为“存在问题学术论文”的概率;
,求抽检一篇学术论文,被认定为“存在问题学术论文”的概率;
(2)现拟定每篇抽检论文不需要复评的评审费用为900元,需要复评的总评审费用1500元;若某次评审抽检论文总数为3000篇,求该次评审费用期望的最大值及对应![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 与双曲线
与双曲线![]() 的公共点,且△
的公共点,且△![]() 的周长为6,求椭圆
的周长为6,求椭圆![]() 的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
(2)如图,已知“盾圆![]() ”的方程为
”的方程为![]() ,设“盾圆
,设“盾圆![]() ”上的任意一点
”上的任意一点![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求证:
,求证:![]() 为定值;
为定值;
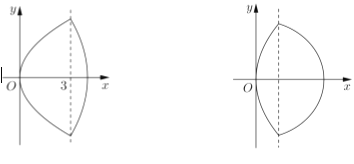
(3)由抛物线弧![]() (
(![]() )与第(1)小题椭圆弧
)与第(1)小题椭圆弧![]()
![]() (
(![]() )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆![]() ”,设过点
”,设过点![]() 的直线与“盾圆
的直线与“盾圆![]() ”交于
”交于![]() 、
、![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() (
(![]() ),试用
),试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)若![]() ,写出
,写出![]() 的单调区间:
的单调区间:
(2)若函数![]() 恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
(3)若函数![]() 在
在![]() 上有四个不同零点
上有四个不同零点![]() ,求
,求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com