
【题目】已知关于![]() 的不等式
的不等式![]() .
.
(1)是否存在![]() 使对所有的实数
使对所有的实数![]() ,不等式恒成立?若存在,求出
,不等式恒成立?若存在,求出![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(2)设不等式对于满足![]() 的一切
的一切![]() 的值都成立,求
的值都成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)记![]() ,那么当
,那么当![]() 时,是否存在区间
时,是否存在区间![]() 使得函数在区间
使得函数在区间![]() 上的值域恰好为
上的值域恰好为![]() ?若存在,请求出区间
?若存在,请求出区间![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由
交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆上任意一点到右焦点
,椭圆上任意一点到右焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(1)求椭圆的方程;
(2)已知点![]() 是线段
是线段![]() 上异于
上异于![]() 的一个定点(
的一个定点(![]() 为坐标原点),是否存在过点
为坐标原点),是否存在过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆交于
与椭圆交于![]() 两点,使得
两点,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定:大桥上的车距![]() 与车速
与车速![]() 和车长
和车长![]() 的关系满足
的关系满足![]() 为正的常数).假定车身长为
为正的常数).假定车身长为![]() ,当车速为
,当车速为![]() 时,车距为
时,车距为![]() 个车身长.
个车身长.
(1)写出车距![]() 关于车速
关于车速![]() 的函数关系式;
的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=![]() a,
a,
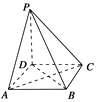
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆的焦点,直线
是椭圆的焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com