
【题目】已知定义在区间(0,+∞)上的函数f(x)满足![]() =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)证明:f(x)为单调递减函数.
(2)若f(3)=-1,求f(x)在[2,9]上的最小值.
【答案】(1)见解析(2)-2
【解析】
(1)任取任取x1,x2∈(0,+∞),且x1>x2,进而可得![]() >1,接下来结合已知即可确定
>1,接下来结合已知即可确定![]() 与
与![]() 的大小关系,从而证得结果;
的大小关系,从而证得结果;
(2)由(1)的结论可知![]() 的最小值是
的最小值是![]() ,接下来结合已知可得
,接下来结合已知可得![]() ,据此即可求得
,据此即可求得![]() 的值,得到结果.
的值,得到结果.
解:(1)证明:任取x1,x2∈(0,+∞),且x1>x2,
则![]() >1,由于当x>1时,f(x)<0,
>1,由于当x>1时,f(x)<0,
所以f![]() <0,即f(x1)-f(x2)<0,
<0,即f(x1)-f(x2)<0,
因此f(x1)<f(x2),
所以函数f(x)在区间(0,+∞)上是单调递减函数.
(2)因为f(x)在(0,+∞)上是单调递减函数,
所以f(x)在[2,9]上的最小值为f(9).
由f![]() =f(x1)-f(x2)得,
=f(x1)-f(x2)得,
f![]() =f(9)-f(3),而f(3)=-1,
=f(9)-f(3),而f(3)=-1,
所以f(9)=-2.
所以f(x)在[2,9]上的最小值为-2.


科目:高中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市出台了相关政策:由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生按照相关政策投资销售一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量y(单位:件)与销售单价x(单位:元)之间的关系近似满足一次函数:![]() .
.
(1)设他每月获得的利润为w(单位:元),写出他每月获得的利润w与销售单价x的函数关系.
(2)相关部门规定,这种节能灯的销售单价不得高于25元.如果他想要每月获得的利润不少于3000元,那么政府每个月为他承担的总差价的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左顶点
的左顶点![]() 和上顶点
和上顶点![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点。
两点。
(1)求椭圆方程;
(2)求线段![]() 的长度的最小值;
的长度的最小值;
(3)当线段![]() 的长度最小时,在椭圆上有两点
的长度最小时,在椭圆上有两点![]() ,使得
,使得![]() ,
,![]() 的面积都为
的面积都为![]() ,求直线
,求直线![]() 在y轴上的截距。
在y轴上的截距。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 实数
实数![]() 使得函数
使得函数![]() 在定义域内为增函数;
在定义域内为增函数;![]() 实数
实数![]() 使得函数
使得函数![]() 在
在![]() 上存在两个零点
上存在两个零点![]() ,且
,且![]()
![]() 分别求出条件
分别求出条件![]() 中的实数
中的实数![]() 的取值范围;
的取值范围;
![]() 甲同学认为“
甲同学认为“![]() 是
是![]() 的充分条件”,乙同学认为“
的充分条件”,乙同学认为“![]() 是
是![]() 的必要条件”,请判断两位同学的说法是否正确,并说明理由.
的必要条件”,请判断两位同学的说法是否正确,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”的关注程度,某机构随机抽取了年龄在20—70岁之间的100人进行调查,经统计“年轻人”与“中老年人”的人数之比为![]() 。
。
关注 | 不关注 | 合计 | |
年轻人 | 30 | ||
中老年人 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有99﹪的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄有关?
列联表,并判断能否有99﹪的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄有关?
(2)现已经用分层抽样的办法从中老年人中选取了6人进行问卷调查,若再从这6人中选取3人进行面对面询问,记选取的3人中关注“中国湖北(潜江)龙虾节”的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
附:参考公式![]() 其中
其中![]() 。
。
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数,
是奇函数,![]() 为偶函数,
为偶函数,![]() 且(e是自然对数的底数).
且(e是自然对数的底数).
(1)分别求出![]() 和
和![]() 的解析式;
的解析式;
(2)记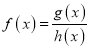 ,请判断
,请判断![]() 的奇偶性和单调性,并分别说明理由;
的奇偶性和单调性,并分别说明理由;
(3)若存在![]() ,使得不等式
,使得不等式![]() 能成立,求实数m的取值范围.
能成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com