
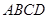 中,
中,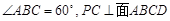 ,
,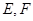 是
是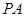 和
和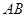 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面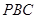 ;
;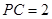 ,求
,求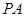 与平面
与平面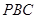 所成角的正弦值.
所成角的正弦值.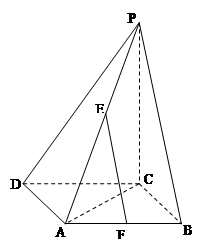
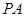 与平面
与平面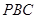 所成的角的正弦值为
所成的角的正弦值为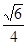 。
。 ,取BC的中点M,连接PM,AM,由题目条件可知
,取BC的中点M,连接PM,AM,由题目条件可知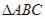 是正三角形,所以
是正三角形,所以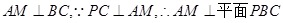 ,所以
,所以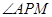 就是直线PA与平面PBC所成的角,然后解三角形即可求出此角.
就是直线PA与平面PBC所成的角,然后解三角形即可求出此角.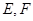 是
是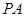 和
和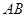 的中点.
的中点.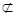 平面PBC,PB
平面PBC,PB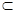 平面PBC……………4
平面PBC……………4 平面
平面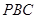 ;………………………….5
;………………………….5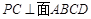 , AH
, AH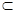 平面ABCD
平面ABCD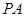 与平面
与平面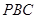 所成的角.----------------9
所成的角.----------------9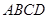 中,
中,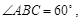 ∴
∴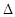 ABC为正三角形, 又AH⊥BC
ABC为正三角形, 又AH⊥BC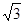 ,……………………………10
,……………………………10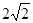 …………………………………11
…………………………………11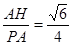
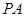 与平面
与平面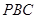 所成的角的正弦值为
所成的角的正弦值为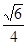 ………………13
………………13

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源:不详 题型:解答题
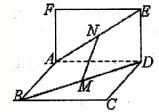
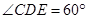 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,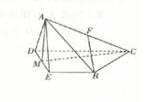
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
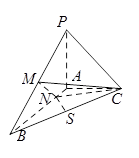
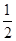 AB,
AB,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
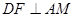 ,垂足为E,若将
,垂足为E,若将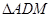 沿AM折起,使点D位于
沿AM折起,使点D位于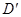 位置,连接
位置,连接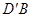 ,
,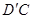 得四棱锥
得四棱锥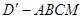 .
.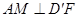 ;(2)若
;(2)若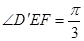 ,直线
,直线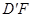 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为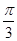 ,求直线
,求直线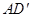 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.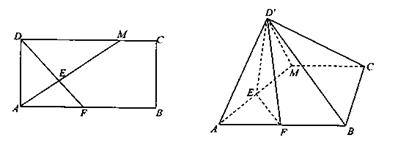
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
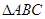 中,
中,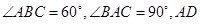 是
是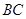 上的高,沿
上的高,沿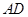 把
把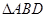 折起,使
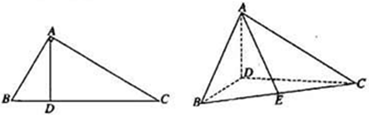
折起,使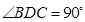 。
。
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
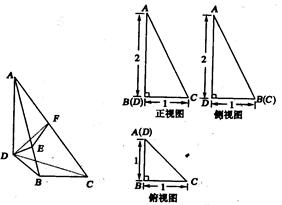
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com