练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数y＝f(x)是定义在R上的增函数，y＝f(x)的图像经过(0，－1)和下面哪一个点时，能使不等式－1＜f(x＋1)＜1的解集为{x|－1＜x＜3}

    [　　]

    A．(3，2)

    B．(4，0)

    C．(3，1)

    D．(4，1)

    答案：D
    解析：

    ∵函数y＝f(x)是定义在R上的增函数，∴函数y＝f(x＋1)也是定义在R上的增函数．∴当－1＜x＜3时，有f(－1＋1)＜f(x＋1)＜f(3＋1)，即f(0)＜f(x＋1)＜f(4)，又能使不等式－1＜f(x＋1)＜1的解集为{x|－1＜x＜3}，则有f(0)＝－1，f(4)＝1，即函数y＝f(x)的图像经过(4，1)．故选D．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：044

    已知：如图射线OA为y＝kx(k＞0，x＞0)，射线OB为y＝－kx(x＞0)，动点P(x，y)在∠AOx的内部，PM⊥OA于M，PN⊥OB于N，四边形ONPM的面积恰为k．

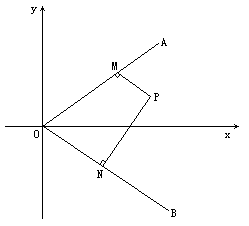
    (Ⅰ)当k为定值时，动点P的纵坐标y是其横坐标x的函数，求这个函数y＝f(x)的解析式；

    (Ⅱ)根据k的取值范围，确定y＝f(x)的定义域．

    查看答案和解析>>

    科目：高中数学 来源：广东省汕头市澄海中学2009－2010学年高一上学期期中考试数学试题 题型：044

    某服装批发商场经营的某种服装，进货成本40元/件，对外批发价定为60元/件．该商场为了鼓励购买者大批量购买，推出优惠政策：一次购买不超过50件时，只享受批发价；一次购买超过50件时，每多购买1件，购买者所购买的所有服装可在享受批发价的基础上，再降低0.1元/件，但最低价不低于50元/件．

    (1)问一次购买多少件时，售价恰好是50元/件？

    (2)设购买者一次购买x件，商场的利润为y元(利润＝销售总额－成本)，试写出函数y＝f(x)的表达式．并说明在售价高于50元/件时，购买者一次购买多少件，商场利润最大．

    查看答案和解析>>

    科目：高中数学 来源：宁夏银川二中2011届高三第一次月考数学理科试题 题型：022

    已知函数y＝f(x)是偶函数，y＝g(x)是奇函数，它们的定域[－π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式＜0的解集是________．

    查看答案和解析>>

    科目：高中数学 来源：山东省济宁市某中学2012届高三9月月考数学试题 题型：044

    为了迎接世博会，某旅游区提倡低碳生活，在景区提供自行车出租．该景区有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元．根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超出6元，则每超过1元，租不出的自行车就增加3辆．为了便于结算，每辆自行车的日租金x(元)只取整数，并且要求出租自行车一日的总收入必须高于这一日的管理费用，用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)．

    (1)求函数y＝f(x)的解析式及其定义域；

    (2)试问当每辆自行车的日租金定为多少元时，才能使一日的净收入最多？

    查看答案和解析>>

    科目：高中数学 来源：2008年普通高等学校招生全国统一考试宁夏卷数学理科 题型：044

    设函数f(x)＝ax＋(a，b∈Z)，曲线y＝f(x)在点(0，f(2))处的切线方程为y＝3．

    (Ⅰ)求f(x)的解析式：

    (Ⅱ)证明：函数y＝f(x)的图像是一个中心对称图形，并求其对称中心；

    (Ⅲ)证明：曲线y＝f(x)上任一点的切线与直线x＝1和直线y＝x所围三角形的面积为定值，并求出此定值．

    查看答案和解析>>

    同步练习册答案