【答案】
分析:(1)利用配方法求函数y=g
3(x)-f(x)的单调区间;
(2)由已知得,
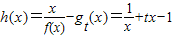
,利用单调性的定义,可知要使h(x)在(0,2]上是单调递减的,必须h(x
1)-h(x
2)>0恒成立,从而只需1-tx
1x
2>0恒成立,即
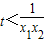
恒成立,故可求实数t的取值范围;(3)解法一:由f(x)<mg
2(x),得x
2<m(-2x+1),分离参数可得
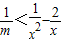
,从而问题转化为
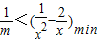
,
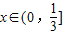
,利用配方法可求函数
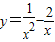
的最小值3,故可求正数m的取值范围;
解法二:由f(x)<mg
2(x),得x
2+2mx-m<0.构造f(x)=x
2+2mx-m,则f(x)<0对任意
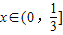
恒成立,只需
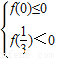
,即
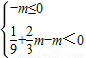
,从而可求正数m的取值范围.
解答:解:(1)y=g
3(x)-f(x)=
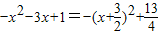
…(1分)
所以函数y的单调递增区间是

,单调递减区间是
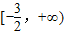
.…(3分)
(2)由已知得,
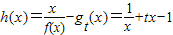
,…(4分)
设0<x
1<x
2≤2,
则

=
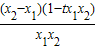
…(6分)
要使h(x)在(0,2]上是单调递减的,必须h(x
1)-h(x
2)>0恒成立. …(7分)
因为x
2-x
1>0,0<x
1x
2<4,
所以1-tx
1x
2>0恒成立,即
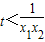
恒成立,…(8分)[
因为

,所以
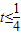
,
所以实数t的取值范围是
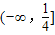
.…(9分)
(3)解法一:由f(x)<mg
2(x),得x
2<m(-2x+1),①…(10分)
因为m>0且
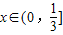
,所以①式可化为
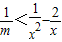
,②…(11分)
要使②式对任意
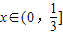
恒成立,只需
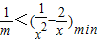
,
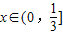
(12分)
因为
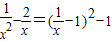
,所以当
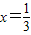
时,函数
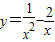
取得最小值3,…(12分)
所以
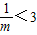
,又m>0,所以
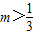
,
故正数m的取值范围是
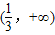
.…(13分)
解法二:由f(x)<mg
2(x),得x
2+2mx-m<0,…(10分)
令f(x)=x
2+2mx-m,则f(x)<0对任意
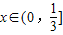
恒成立,…(11分)
只需
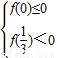
,即
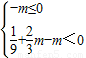
,解得
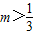
,…(12分)
故正数m的取值范围是
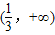
. …(13分)
点评:本题考查的重点是求参数的范围问题,考查恒成立问题,考查函数的单调区间,解题的关键是利用分离参数法,进而求函数的最值.

 在(0,2]上是单调递减的,求实数t的取值范围;
在(0,2]上是单调递减的,求实数t的取值范围; 恒成立,求正数m的取值范围.
恒成立,求正数m的取值范围.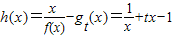 ,利用单调性的定义,可知要使h(x)在(0,2]上是单调递减的,必须h(x1)-h(x2)>0恒成立,从而只需1-tx1x2>0恒成立,即
,利用单调性的定义,可知要使h(x)在(0,2]上是单调递减的,必须h(x1)-h(x2)>0恒成立,从而只需1-tx1x2>0恒成立,即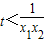 恒成立,故可求实数t的取值范围;(3)解法一:由f(x)<mg2(x),得x2<m(-2x+1),分离参数可得
恒成立,故可求实数t的取值范围;(3)解法一:由f(x)<mg2(x),得x2<m(-2x+1),分离参数可得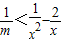 ,从而问题转化为
,从而问题转化为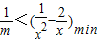 ,
,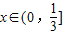 ,利用配方法可求函数
,利用配方法可求函数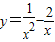 的最小值3,故可求正数m的取值范围;
的最小值3,故可求正数m的取值范围;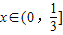 恒成立,只需
恒成立,只需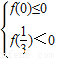 ,即
,即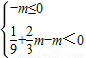 ,从而可求正数m的取值范围.
,从而可求正数m的取值范围.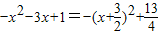 …(1分)
…(1分) ,单调递减区间是
,单调递减区间是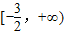 .…(3分)
.…(3分)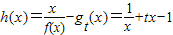 ,…(4分)
,…(4分) =
=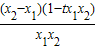 …(6分)
…(6分)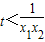 恒成立,…(8分)[
恒成立,…(8分)[ ,所以
,所以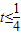 ,
,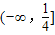 .…(9分)
.…(9分)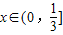 ,所以①式可化为
,所以①式可化为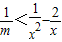 ,②…(11分)
,②…(11分)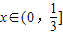 恒成立,只需
恒成立,只需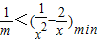 ,
,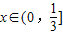 (12分)
(12分)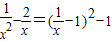 ,所以当
,所以当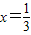 时,函数
时,函数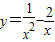 取得最小值3,…(12分)
取得最小值3,…(12分)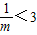 ,又m>0,所以
,又m>0,所以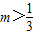 ,
,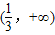 .…(13分)
.…(13分)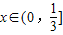 恒成立,…(11分)
恒成立,…(11分)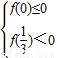 ,即
,即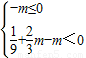 ,解得
,解得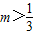 ,…(12分)
,…(12分)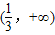 . …(13分)
. …(13分)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<