
【题目】某火锅店为了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如表:

(1)求y关于x的回归方程![]() ;
;
(2)判定y与x之间是正相关还是负相关,若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额.
科目:高中数学 来源: 题型:
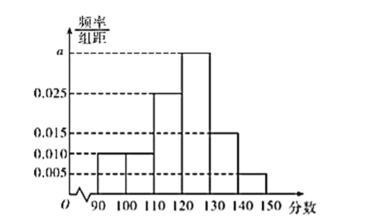
【题目】某校高二年级共有800名学生参加了数学测验(满分150分),已知这800名学生的数学成绩均不低于90分,将这800名学生的数学成绩分组如:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到的频率分布直方图如图所示,则下列说法中正确的是( )
,得到的频率分布直方图如图所示,则下列说法中正确的是( )
①![]() ;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,各个侧面均是边长为
中,各个侧面均是边长为![]() 的正方形,
的正方形,![]() 为线段
为线段![]() 的中点
的中点

(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求证:直线![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设![]() 为线段
为线段![]() 上任意一点,在
上任意一点,在![]() 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点![]() ,使
,使![]() ,并说明理由
,并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,
,![]() ,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若
,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若![]() 平面ABC,则三棱锥
平面ABC,则三棱锥![]() 的四个面都是直角三角形;②若
的四个面都是直角三角形;②若![]() 平面ABC,且M是边AB的中点,则有
平面ABC,且M是边AB的中点,则有![]() ;③若
;③若![]() ,
,![]() 平面ABC,则
平面ABC,则![]() 面积的最小值为
面积的最小值为![]() ;④若
;④若![]() ,P在平面ABC上的射影是
,P在平面ABC上的射影是![]() 内切圆的圆心,则点P到平面ABC的距离为
内切圆的圆心,则点P到平面ABC的距离为![]() .其中正确命题的序号是________.(把你认为正确命题的序号都填上)
.其中正确命题的序号是________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com