
【题目】如图1,在长方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点.现将
上一动点.现将![]() 沿
沿![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.
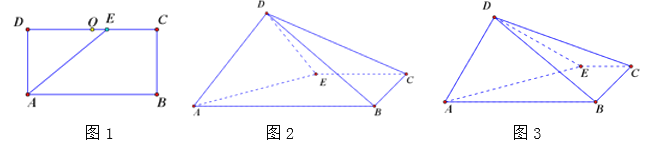
(1)若![]() 与
与![]() 重合,且
重合,且![]() (如图2).证明:
(如图2).证明:![]() 平面
平面![]() ;
;
(2)若![]() 不与
不与![]() 重合,且平面
重合,且平面![]() 平面
平面![]() (如图3),设
(如图3),设![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;
(2)![]() .
.
【解析】
(1)由AD⊥BD,AD⊥DE,BD∩DE=D,可得AD⊥平面BDE,可得AD⊥BE.由E与O重合,可得△ADE与△BCE都为等腰直角三角形,可得BE⊥AE.即可证明结论.
(2)过E点作EH⊥AB,垂足为H,并连接DH,证明EH⊥DH,设CE=x,则DE=4﹣x,在Rt△DHB中列出t关于x的函数关系式,利用二次函数求最值即可
(1)由![]() 与
与![]() 重合,则有
重合,则有![]() , 因为AD⊥BD,
, 因为AD⊥BD,![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() .
.
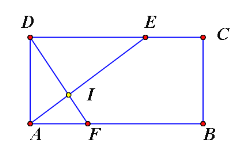

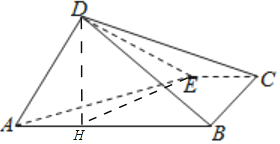
(2)如图过E点作EH⊥AB,垂足为H,并连接DH,
又∵平面ABD⊥平面ABC,平面ABD∩平面ABC=AB,EH平面ABC,
∴EH⊥平面ABD,∵DH平面ABD,∴EH⊥DH,
设CE=x,则DE=4﹣x,
∵BC⊥AB,∴BC∥EH,又CE∥AB,∴BH=x,EH=2,
∴在Rt△DHE中,DH![]() ,
,
∴在Rt△DHB中,t![]() ,
,
∵x∈[0,2),∴t∈![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.
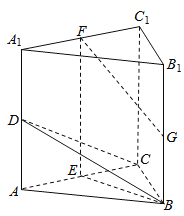
(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视台应某企业之约播放两套连续剧,其中,连续剧甲每次播放时间80分钟,其中广告时间1分钟,收视观众60万;连续剧乙每次播放时间40分钟,其中广告时间1分钟,收视观众20万.现在企业要求每周至少播放广告6分钟,而电视台每周至多提供320分钟节目时间.
(1)设每周安排连续剧甲![]() 次,连续剧乙
次,连续剧乙![]() 次,列出
次,列出![]() ,
,![]() 所应该满足的条件;
所应该满足的条件;
(2)应该每周安排两套电视剧各多少次,收视观众最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量![]() ,
,![]() ,令函数
,令函数![]() ,若函数
,若函数![]() 的部分图象如图所示,且点
的部分图象如图所示,且点![]() 的坐标为
的坐标为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)求函数![]() 的单调增区间及对称轴方程;
的单调增区间及对称轴方程;
(3)若把方程![]() 的正实根从小到大依次排列为
的正实根从小到大依次排列为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和直线
和直线![]() ,
,![]() 为曲线
为曲线![]() 上一点,
上一点,![]() 为点
为点![]() 到直线
到直线![]() 的距离且满足
的距离且满足![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作曲线
作曲线![]() 的两条动弦
的两条动弦![]() ,若直线
,若直线![]() 斜率之积为
斜率之积为![]() ,试问直线
,试问直线![]() 是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com