
| 6 |
| a |
| a2 | |||||
|
| 5 |
| 6 |
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 4 |
| 1 |
| 2 |
| 6 |
| a |
| a2 | |||||
|
| 7 |
| 6 |
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 6 |
| a |
| 6 |
| a |
| a2 | |||||
|
| 7 |
| 6 |
| 1+x2 |
| 1-x2 |
| 1 |
| x |
| 1+x2 |
| 1-x2 |
1+
| ||
1-
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|


科目:高中数学 来源: 题型:
| 6 |
| a |
| DB |
| DC |
| DA |
| AB |
| AC |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2015届湖北省荆门市高一上学期期末教学质量检测数学试卷(解析版) 题型:填空题
有下列叙述:
①集合 中只有四个元素;
中只有四个元素;
② 在其定义域内为增函数;
在其定义域内为增函数;
③已知 ,则角
,则角 的终边落在第四象限;
的终边落在第四象限;
④平面上有四个互异的点 ,且点
,且点 不共线,已知
不共线,已知 ,则△
,则△ 是等腰三角形;
是等腰三角形;
⑤若函数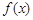 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 .
.
其中所有正确叙述的序号是 .
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 6 |
| a |
| DB |
| DC |
| DA |
| AB |
| AC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com