分析:(1)过A作AQ∥C
1N,交A
1C
1于Q,连接B
1Q,可得∠B
1AQ(或其补角)是异面直线AB
1与C
1N所成角.在△B
1AQ中,分别求出AB
1、AQ和B
1Q的长,结合余弦定理算出cos∠B
1AQ的值,从而得到异面直线AB
1与C
1N所成的角是arccos
;
(2)平面A
1B
1C
1中,过M作MH⊥A
1C
1于H.根据直三棱柱的性质结合面面垂直的性质定理,得到MH⊥平面AA
1C
1C,MH是三棱锥M-C
1CN的高.算出MH的长和△C
1CN的面积,结合三棱锥的体积公式,可得三棱锥M-C
1CN的体积.
解答:解:(1)平面AA
1C
1C中,过A作AQ∥C
1N,交A
1C
1于Q,连接B
1Q
∴∠B
1AQ(或其补角)就是异面直线AB
1与C
1N所成的角
矩形AA
1C
1C中,N是AC中点,可得Q是A
1C
1中点
Rt△AA
1B
1中,AB
1=
=5,同理可得AQ=
∵等腰Rt△A
1B
1C
1中,B
1Q是斜边的中线
∴B
1Q=
A
1B
1=2
,
△B
1AQ中,cos∠B
1AQ=
=
>0
∴∠B
1AQ=arccos
,即异面直线AB
1与C
1N所成的角等于arccos
;
(2)平面A
1B
1C
1中,过M作MH⊥A
1C
1于H
∵直三棱柱ABC-A
1B
1C
1中,CC
1⊥平面A
1B
1C
1,CC
1⊆平面AA
1C
1C
∴平面AA
1C
1C⊥平面A
1B
1C
1,
∵平面AA
1C
1C⊥平面A
1B
1C
1=A
1C
1,MH⊥A
1C
1,
∴MH⊥平面AA
1C
1C,MH是三棱锥M-C
1CN的高线
∵△B
1C
1Q中,M是B
1C
1中点,MH∥B
1Q
∴MH是△B
1C
1Q的中位线,得MH=
B
1Q=
∵△C
1CN的面积S=
CN×C
1C=
×2
×3=3
∴三棱锥M-C
1CN的体积V
M-C1CN=
S
C1CN×MH=
×3
×
=2
点评:本题给出特殊三棱柱,求异面直线所成角并求锥体的体积,着重考查了线面垂直、面面垂直的判定与性质,异面直线所成角的求法和锥体体积公式等知识,属于基础题.

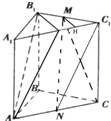
 (2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.
(2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.


 阅读快车系列答案
阅读快车系列答案