
分析 化简曲线方程,作出曲线图象,根据直线与曲线的交点个数求出k的范围.
解答 解:∵$\sqrt{1-{{(x-1)}^2}}$=|y-1|-2,
∴$\sqrt{1-{{(x-1)}^2}}$=y-3(y≥3)与$\sqrt{1-{{(x-1)}^2}}$=-1-y(y≤-1),
∴(x-1)2+(y-3)2=1(y≥1)或(x-1)2+(y+1)2=1(y≤-1).
∴曲线$\sqrt{1-{{(x-1)}^2}}$=|y-1|-2表示以(1,3)为圆心以1为半径的上半圆和以(1,-1)为圆心,以1为半径的下半圆.
作出图形如下: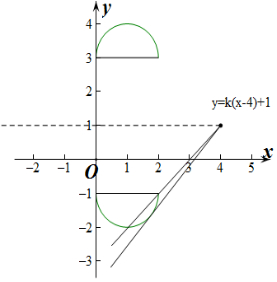
设直线y=k(x-4)+1过点(2,-1),则-2k+1=-1,∴k=1.
若直线y=k(x-4)+1与半圆(x-1)2+(y+1)2=1(y≤-1)相切.
则$\frac{|-3k+2|}{\sqrt{{k}^{2}+1}}$=1,解得k=$\frac{3+\sqrt{3}}{4}$(舍)或k=$\frac{3-\sqrt{3}}{4}$.
∴当直线y=k(x-4)+1与半圆(x-1)2+(y+1)2=1(y≤-1)有两个交点时,
1≤k<$\frac{3-\sqrt{3}}{4}$,
∵直线y=k(x-4)+1过点(4,1),且两个半圆关于直线y=1对称,
∴当直线y=k(x-4)+1与半圆(x-1)2+(y-3)2=1(y≥3)有两个交点时,
k的范围是-$\frac{3-\sqrt{3}}{4}$<k≤1.
∴k的取值范围是1≤k<$\frac{3-\sqrt{3}}{4}$或-$\frac{3-\sqrt{3}}{4}$<k≤-1.
故答案为(-$\frac{3-\sqrt{3}}{4}$,-1]∪[1,$\frac{3-\sqrt{3}}{4}$).
点评 本题考查了圆的方程,直线与圆的位置关系,属于中档题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
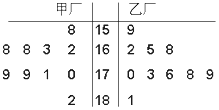 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
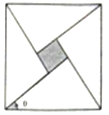 我国古代数学家赵爽利用“勾股圈方图”巧妙的证明了勾股定理,成就了我国古代数学的骄傲,后人称之为“赵爽弦图”.他是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形,若直角三角形中较小的锐角记为θ,大正方形的面积为25,小正方形的面积为1,则$sin\frac{θ}{2}+cos\frac{θ}{2}$=$\frac{{2\sqrt{10}}}{5}$.
我国古代数学家赵爽利用“勾股圈方图”巧妙的证明了勾股定理,成就了我国古代数学的骄傲,后人称之为“赵爽弦图”.他是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形,若直角三角形中较小的锐角记为θ,大正方形的面积为25,小正方形的面积为1,则$sin\frac{θ}{2}+cos\frac{θ}{2}$=$\frac{{2\sqrt{10}}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com