练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用五种不同的颜色给图中4个区域涂色，如果每一区域涂一种颜色，相邻区域不能同色，那么共有________种涂色方法．

    答案：180
    解析：

    解 区域2，4不同色，先涂区域2有5种办法，再涂区域4有4种办法；剩下三种颜色涂区域1，3，各有3种办法，根据乘法原理，得5×4×3×3＝180种办法．


    提示：

    注 本题要注意与例2的区别．也可分用四种颜色、三种颜色两类情况列式计算．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

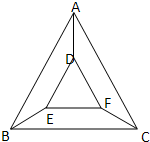    如图，用五种不同的颜色给图中的A、B、C、D、E、F六个不同的点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共（　　）种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

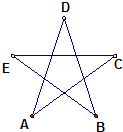
    用五种不同的颜色给图中的“五角星”的五个顶点染色，（每点染一色，有的颜色也可以不用）使每条线段上的两个顶点皆不同色，则不同的染色方法有
    1020
    1020
    种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    用五种不同的颜色给图中标有①②③④的各部分涂色,相邻部分涂不同的色,则涂色的方法共有(    )

    A.96种           B.120种             C.192种          D.240种

    查看答案和解析>>

    科目：高中数学 来源：2014届重庆市高二下学期期中考试理科数学试卷（解析版） 题型：选择题

    如图，用五种不同的颜色给图中的A、B、C、D、E、F六个不同的点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共（    ）种。

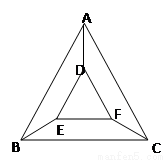
    A、1240       B、360       C、1920       D、264

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    用五种不同的颜色给图中的“五角星”的五个顶点染色，（每点染一色，有的颜色也可以不用）使每条线段上的两个顶点皆不同色，则不同的染色方法有______种．
    精英家教网

    查看答案和解析>>

    同步练习册答案