
【题目】设有下列四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :“
:“![]() ”是“
”是“![]() 为奇函数”的充要条件;
为奇函数”的充要条件;
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件.
是递减数列”的充要条件.
其中,真命题的是![]()
![]()
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设有关于![]() 的一元二次方程
的一元二次方程![]() .
.
(Ⅰ)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,A是椭圆短轴的一个端点,直线AF与椭圆另一交点为B,且
,A是椭圆短轴的一个端点,直线AF与椭圆另一交点为B,且![]() .
.
(1)求椭圆方程;
(2)若斜率为1的直线l交椭圆于C,D,且CD为底边的等腰三角形的顶点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
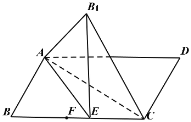
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点且满足
上一点且满足![]() ,
,![]() 是线段
是线段![]() 上一动点,把
上一动点,把![]() 沿
沿![]() 折起得到
折起得到![]() ,使得平面
,使得平面![]() 平面
平面![]() ,分别记
,分别记![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 所成锐角为
所成锐角为![]() ,则:( )
,则:( )

![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 交于点
交于点![]() ,曲线
,曲线![]() 与
与![]() 轴交于点
轴交于点![]() ,求线段
,求线段![]() 的中点到点
的中点到点![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了分析某个高三学生的学习状态.现对他前5次考试的数学成绩x,物理成绩y进行分析.下面是该生前5次考试的成绩.
数学 | 120 | 118 | 116 | 122 | 124 |
物理 | 79 | 79 | 77 | 82 | 83 |
附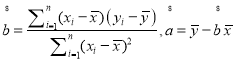 .
.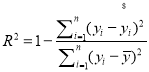 .
.
![]() 已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
![]() 我们常用
我们常用![]() 来刻画回归的效果,其中
来刻画回归的效果,其中![]() 越接近于1,表示回归效果越好.求
越接近于1,表示回归效果越好.求![]() .
.
![]() 已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在射线
在射线![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com