练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，角A、B均为锐角，则cosA＞sinB是△ABC为钝角三角形的（ ）
    A.充分不必要条件
    B.必要不充分条件
    C.充要条件
    D.既不充分也不必要条件

    【答案】C
    【解析】解：因为cosA＜sinB，所以cosA＞cos（ ﹣B）， 又因为角A，B均为锐角，所以 ﹣B为锐角，
    又因为余弦函数在（0，π）上单调递减，
    所以A＜ ﹣B，所以A+B＜
    △ABC中，A+B+C=π，所以C＞ ，
    所以△ABC为钝角三角形，
    若△ABC为钝角三角形，角A、B均为锐角
    所以C＞ ，
    所以A+B＜
    所以A＜ ﹣B，
    所以cosA＞cos（ ﹣B），
    即cosA＞sinB
    故cosA＞sinB是△ABC为钝角三角形的充要条件．
    故选：C
    利用诱导公式cos（ ﹣α）=sinα及余弦函数的单调性和充要条件的定义可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）若 ，讨论函数 的单调性；
    （2）曲线 与直线 交于 ， 两点，其中 ，若直线 斜率为 ，求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某自行车厂为共享单车公司生产新样式的单车，已知生产新样式单车的固定成本为20000元，每生产一件新样式单车需要增加投入100元．根据初步测算，自行车厂的总收益（单位：元）满足分段函数h（x），其中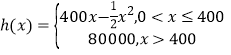,x是新样式单车的月产量（单位：件），利润=总收益﹣总成本．

    （1）试将自行车厂的利润y元表示为月产量x的函数；

    （2）当月产量为多少件时自行车厂的利润最大？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=loga（1+x），g（x）=loga（1﹣x），（a＞1）．

    （1）求函数h(x)=f（x）﹣g（x）的定义域；

    （2）求使f（x）﹣g（x）＞0的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率e＝，连接椭圆的四个顶点得到的菱形的面积为4.

    (1)求椭圆的方程；

    (2)设直线过椭圆的左端点A，与椭圆的另一个交点为B.，AB的垂直平分线交轴于点，且·＝4，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数f（x）= ，设f2（x）=f[f（x）]，f3（x）=f[f2（x）]，…，fn+1（x）=f[fn（x）]（n∈N* ， 且n≥2），令集合M={x|f2036（x）=x，x∈R}，则集合M为（ ）
    A.空集
    B.实数集
    C.单元素集
    D.二元素集

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex（x﹣aex）有两个极值点，则实数a的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，椭圆C： + =1（a＞b＞0）的离心率e= ，且点P（2，1）在椭圆C上． （Ⅰ）求椭圆C的方程；
    （Ⅱ）若点A、B都在椭圆C上，且AB中点M在线段OP（不包括端点）上．求△AOB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，圆C的参数方程为 ，（t为参数），在以原点O为极点，x轴的非负半轴为极轴建立的极坐标系中，直线l的极坐标方程为 ，A，B两点的极坐标分别为 ．
    （1）求圆C的普通方程和直线l的直角坐标方程；
    （2）点P是圆C上任一点，求△PAB面积的最小值．

    查看答案和解析>>

    同步练习册答案