
【题目】已知命题p:方程x2+y2﹣ax+y+1=0表示圆;命题q:方程2ax+(1﹣a)y+1=0表示斜率大于1的直线,若p∨q为真命题,p∧q为假命题,求a的取值范围.
【答案】解:若x2+y2﹣ax+y+1=0表示圆,
则a2+1﹣4>0,
解得:a∈(﹣∞, ![]() )∪(
)∪( ![]() ,+∞),
,+∞),
故命题p:a∈(﹣∞, ![]() )∪(
)∪( ![]() ,+∞),
,+∞),
若方程2ax+(1﹣a)y+1=0表示斜率大于1的直线,
则 ![]() >1解得:a∈(﹣∞,﹣1)∪(1,+∞),
>1解得:a∈(﹣∞,﹣1)∪(1,+∞),
故命题q:a∈(﹣∞,﹣1)∪(1,+∞),
若p∨q为真命题,p∧q为假命题,
则p,q一真一假;
当p真q假时,a∈(﹣∞, ![]() )∪(
)∪( ![]() ,+∞)且a∈[﹣1,1],不存在满足条件的a值;
,+∞)且a∈[﹣1,1],不存在满足条件的a值;
当p假q真时,a∈[﹣ ![]() ,
, ![]() ]且a∈(﹣∞,﹣1)∪(1,+∞),
]且a∈(﹣∞,﹣1)∪(1,+∞),
故a∈[﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() ]
]
【解析】若命题p∨q为真命题,p∧q,命题p,q一真一假,进而可得满足条件的a的取值范围.
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案,需要熟知两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= ![]() PD.
PD.
(Ⅰ)证明:平面PQC⊥平面DCQ
(Ⅱ)求二面角Q﹣BP﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某建材公司在![]() ,
,![]() 两地各有一家工厂,它们生产的建材由公司直接运往
两地各有一家工厂,它们生产的建材由公司直接运往![]() 地.由于土路交通运输不便,为了减少运费,该公司预备投资修建一条从
地.由于土路交通运输不便,为了减少运费,该公司预备投资修建一条从![]() 地或
地或![]() 地直达
地直达![]() 地的公路;若选择从某地修建公路,则另外一地生产的建材可先运输至该地再运至
地的公路;若选择从某地修建公路,则另外一地生产的建材可先运输至该地再运至![]() 以节约费用.已知
以节约费用.已知![]() ,
,![]() 之间为土路,土路运费为每吨千米20元,公路的运费减半,
之间为土路,土路运费为每吨千米20元,公路的运费减半,![]() ,
,![]() ,
,![]() 三地距离如图所示.为了制定修路计划,公司统计了最近10天两个工厂每天的建材产量,得到下面的柱形图,以两个工厂在最近10天日产量的频率代替日产量的概率.
三地距离如图所示.为了制定修路计划,公司统计了最近10天两个工厂每天的建材产量,得到下面的柱形图,以两个工厂在最近10天日产量的频率代替日产量的概率.
(1)求“![]() ,
,![]() 两地工厂某天的总日产量为20吨”的概率;
两地工厂某天的总日产量为20吨”的概率;
(2)以修路后每天总的运费的期望为依据,判断从![]() ,
,![]() 哪一地修路更加划算.
哪一地修路更加划算.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某种产品的质量(单位:千克),抽取了一个容量为N的样本,整理得到的数据作出了频率分布表和频率分布直方图如图:
分组 | 频数 | 频率 |
[17.5,20) | 10 | 0.05 |
[20,225) | 50 | 0.25 |
[22.5,25) | a | b |
[25,27.5) | 40 | c |
[27.5,30] | 20 | 0.10 |
合计 | N | 1 |
(Ⅰ)求出表中N及a,b,c的值;
(Ⅱ)求频率分布直方图中d的值;
(Ⅲ)从该产品中随机抽取一件,试估计这件产品的质量少于25千克的概率.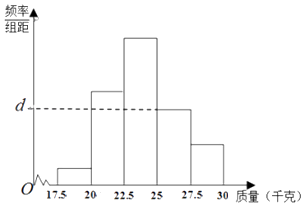
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 若对于任意的正整数n都有Sn=2an﹣3n.
(1)设bn=an+3,求证:数列{bn}是等比数列,并求出{an}的通项公式;
(2)求数列{nan}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com