
分析 (1)求出未租出的车辆数,即可推出租出的辆数.
(2)设每辆车的月租金定为x元,得到租赁公司的月收益为:f(x)=-$\frac{1}{5}$(x-4 05)2+307 05,利用二次函数求解最值即可.
解答 (本小题满分12分)
解:(1)当每辆车的月租金定为3 60元时,未租出的车辆数为$\frac{360-300}{5}$=12,…(2分)
所以这时租出了100-12=88辆车.…(4分)
(2)设每辆车的月租金定为x元,…(5分)
则租赁公司的月收益为:f(x)=$({100\;-\frac{x-300}{5}})$(x-15)-$\frac{x-300}{5}$×5
=$-\frac{1}{5}{x^2}+162x-2100$=-$\frac{1}{5}$(x-405)2+30705.…(8分)
所以,当x=405 时,f(x)最大,其最大值为f(405)=30705.…(11分)
当每辆车的月租金定为405元时,月收益最大,其值为30705元.…(12分)
点评 本题考查实际问题的解决方法,考查函数与方程的应用,二次函数的性质的应用,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -2 | C. | -4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
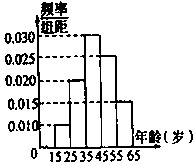 某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的概率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | b | 0.36 |
| 第5组 | [55,65) | 3 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
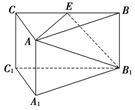 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AE与B1C1是异面直线,且AE⊥B1C1 | ||
| C. | AC⊥平面ABB1A1 | D. | A1C1∥平面AB1E |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com