
【题目】张老师给学生出了一道题,“试写一个程序框图,计算S=1+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是( )
”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是( )
A.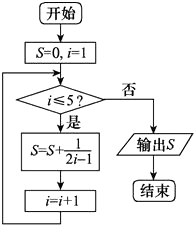
B.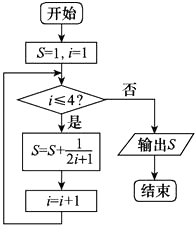
C.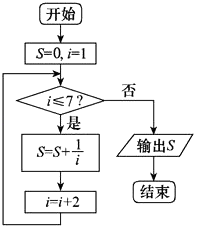
D.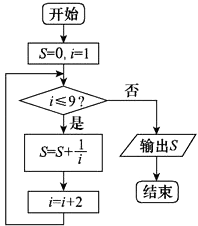
科目:高中数学 来源: 题型:
【题目】【2017徐州考前信息卷20】已知函数![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,其中
恒成立,其中![]() 是自然对数的底数,求
是自然对数的底数,求![]() 的取值范围;
的取值范围;
(3)设曲线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,且两曲线在点
,且两曲线在点![]() 处的切线分别为
处的切线分别为![]() ,
,![]() .试判断
.试判断![]() ,
,![]() 与
与![]() 轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PA⊥底面ABCD,且PA=AB=AD=![]() CD,AB∥CD,∠ADC=90°.
CD,AB∥CD,∠ADC=90°.
(1)在侧棱PC上是否存在一点Q,使BQ∥平面PAD?证明你的结论;
(2)求证:平面PBC⊥平面PCD;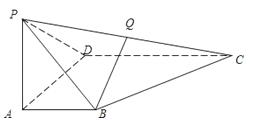
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校今年准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12,则报考飞行员的总人数是 .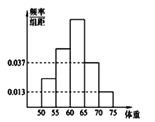
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2﹣(a+1)x+1.
(1)若不等式f(x)<mx的解集为{x|1<x<2},求实数a、m的值;
(2)解不等式f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(ωx+φ)(ω>0,﹣
sin(ωx+φ)(ω>0,﹣ ![]() ≤φ<
≤φ< ![]() ),f(0)=﹣
),f(0)=﹣ ![]() ,且函数f(x)图象上的任意两条对称轴之间距离的最小值是
,且函数f(x)图象上的任意两条对称轴之间距离的最小值是 ![]() .
.
(1)求函数f(x)的解析式;
(2)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求cos(α+
),求cos(α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从高三学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下(单位:分):
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100),8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率分布折线图;
(3)估计成绩在[60,90)分的学生比例;
(4)估计成绩在85分以下的学生比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( ) 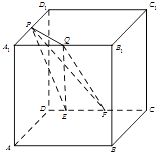
A.点P到平面QEF的距离
B.三棱锥P﹣QEF的体积
C.直线PQ与平面PEF所成的角
D.二面角P﹣EF﹣Q的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,若数列{an}满足![]()
=2kan对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com