
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).![]() 是曲线
是曲线![]() 上的动点,将线段
上的动点,将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(I)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(II)在(I)的条件下,若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点(除极点外),且有定点
两点(除极点外),且有定点![]() ,求
,求![]() 面积.
面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆A:(x+1)2+y2=16,圆C过点B(1,0)且与圆A相切,设圆心C的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)过点B作两条互相垂直的直线l1,l2,直线l1与E交于M,N两点,直线l2与圆A交于P,Q两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(I)求出表中x,y的值;
(II)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
(III)从抽出的女生中再随机抽取3人进一步了解情况,记X为抽取的这3名女生中A类人数和C类人数差的绝对值,求X的数学期望。
附:K2=![]() )
)
P(K2≥k0) | 0.10 | 0.01 | |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点的序列![]() ,其中
,其中![]() .(
.(![]() 是线段
是线段![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,……,
的中点,……,![]() 是线段
是线段![]() 的中点,…)
的中点,…)
(1)写出![]() 与
与![]() 之间的关系
之间的关系![]() ;
;
(2)设![]() ,计算
,计算![]() ,由此推测数列
,由此推测数列![]() 的通项公式,并且加以证明;
的通项公式,并且加以证明;
(3)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如下茎叶图:
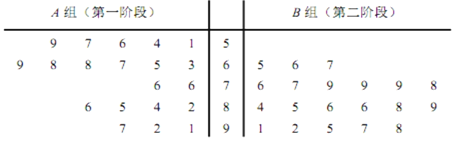
![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 假设两组群众的评价结果相互独立,由频率估计概率,求创文工作第二阶段的民众满意度等级高于第一阶段的概率;
假设两组群众的评价结果相互独立,由频率估计概率,求创文工作第二阶段的民众满意度等级高于第一阶段的概率;
![]() 从这40名群众中随机抽取2人,记X表示满意度等级为“非常满意”的群众人数,求X的分布列与数学期望.
从这40名群众中随机抽取2人,记X表示满意度等级为“非常满意”的群众人数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于直角![]() 在定平面
在定平面![]() 内的射影有如下判断:①可能是的0°角;②可能是锐角;③可能是直角;④可能是钝角;⑤可能是180°的角;其中正确判断的序号是( )
内的射影有如下判断:①可能是的0°角;②可能是锐角;③可能是直角;④可能是钝角;⑤可能是180°的角;其中正确判断的序号是( )
A.②③⑤B.①②③C.①④⑤D.①②③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com