
【题目】在平面直角坐标系xOy中,曲线y=x2-2x—3与两条坐标轴的三个交点都在圆C上.若圆C与直线x-y+a=0交于A,B两点,
(1)求圆C的标准方程;
(2)若 ![]() (O为原点),求a的值.
(O为原点),求a的值.
【答案】. (1)(x-1)2+(y+1)2=5.(2)a=-4
【解析】
(1)先求出曲线y=x2-2x—3与两条坐标轴的三个交点坐标,设圆C的圆心为(1,t),求出t的值和圆的半径,由此能求出圆C的方程.
(2)设A(x1,y1),B(x2,y2),联立直线与圆的方程,根据一元二次方程判别式和韦达定理,以及![]() ,即可求出a 的值.
,即可求出a 的值.
解:(1)曲线y=x2-2x—3与y轴的交点为(0,-3),与x轴的交点为(-1,0),(3,0).
故可设圆C的圆心为(1,t),则有12+(t+3)2=(1+1)2+t2,解得t=![]() .
.
则圆C的半径为![]() .
.
则以圆C的方程为(x-1)2+(y+1)2=5.
(2)设A(x1,y1),B(x2,y2),
其坐标满足方程组:![]() 消去y,得到方程2x2+2ax+a2+2a-3=0.
消去y,得到方程2x2+2ax+a2+2a-3=0.
Δ=24-16a-4a2>0,且x1+x2=-a,x1x2=![]() .①
.①
由![]() 可得x1x2+y1y2=5,又y1=x1+a,y2=x2+a,
可得x1x2+y1y2=5,又y1=x1+a,y2=x2+a,
所以2x1x2+a(x1+x2)+a2=5.②
由①,②得a=-4或a=2 ,
因为满足Δ>0,故a=-4


科目:高中数学 来源: 题型:
【题目】已知在平面坐标系内,O为坐标原点,向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),点M为直线OP上的一个动点.
=(2,1),点M为直线OP上的一个动点.
(1)当 ![]()
![]() 取最小值时,求向量
取最小值时,求向量 ![]() 的坐标;
的坐标;
(2)在点M满足(I)的条件下,求∠AMB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex与g(x)=ax+b的图象交于P(x1 , y1),Q(x2 , y2)两点. (Ⅰ)求函数h(x)=f(x)﹣g(x)的最小值;
(Ⅱ)且PQ的中点为M(x0 , y0),求证:f(x0)<a<y0 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2. 表1
停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
频数 | 26 | a | b | 8 | 2 |
表2
平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
已知表1数据的中位数估计值为26,回答以下问题.
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程 ![]() ;
;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1 , y1),(x2 , y2),…,(xn , yn),其回归直线 ![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为  ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本p(x)=![]() 万元.
万元.
(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量q(m)=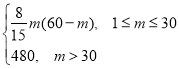 (单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
(单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点. 
(1)证明:三棱锥Q﹣ABP体积VQ﹣ABP≤ ![]() ,并指出P和Q满足什么条件时有AP⊥BQ
,并指出P和Q满足什么条件时有AP⊥BQ
(2)求二面角P﹣AB﹣Q平面角的取值范围,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB= ![]() EA=
EA= ![]() ED,EF∥BD
ED,EF∥BD 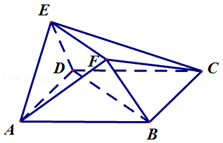
(I)证明:AE⊥CD
(II)在棱ED上是否存在点M,使得直线AM与平面EFBD所成角的正弦值为 ![]() ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com