
| A. | p∨(¬q) | B. | p∨q | C. | p∧q | D. | (¬p)∨(¬q) |
分析 对于命题p:x2>x,解得x>1或x<0,即可判断出真假.命题q:若数列{an}的前n项和Sn=n2,则n=1时,a1=1;n≥2时,an=Sn-Sn-1,解出即可判断出真假.再利用复合命题真假的判定方法即可判断出结论.
解答 解:对于命题p:x2>x,解得x>1或x<0,因此x2>x是x>1的必要不充分条件,因此是假命题.
命题q:若数列{an}的前n项和Sn=n2,则n=1时,a1=1;n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,当n=1时也成立.∴an=2n-1,因此数列{an}是等差数列,首项为1,公差为2,因此是真命题.
∴只有P∨q是真命题.
故选:B.
点评 本题考查了简易逻辑的应用、不等式解法、等差数列的充要条件,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -2≤a≤-1 | B. | -2≤a<-1 | C. | -2<a≤-1 | D. | -2<a<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1)n$\frac{1}{n}$ | B. | (-1)n+1$\frac{1}{n}$ | C. | (-1)n$\frac{1}{n+1}$ | D. | (-1)n+1$\frac{1}{n-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | 2a-b<1 | C. | $\frac{a}{{c}^{2}+1}$>$\frac{b}{{c}^{2}+1}$ | D. | lg(a-b)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为π | B. | 函数f(x)图象关于点$(\frac{5π}{12},0)$对称 | ||
| C. | 函数f(x)在区间$[0,\frac{π}{2}]$上是减函数 | D. | 函数f(x)的图象关于直线$x=\frac{π}{6}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
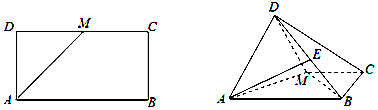
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com