
分析 (1)根据向量的坐标运算,结合模长公式和三角恒等变换,即可求出sin2θ的值;
(2)根据平面向量的坐标表示与向量相等,求出实数m,n的值,代入(m-3)2+n2,利用三角函数的有界性即可计算它的最大值.
解答 解:(1)点$A({1,1}),B({1,-1}),C({\sqrt{2}cosθ,\sqrt{2}sinθ}),θ∈R$,O是坐标原点,
∴$\overrightarrow{BC}$-$\overrightarrow{BA}$=$\overrightarrow{AC}$=($\sqrt{2}$cosθ-1,$\sqrt{2}$sinθ-1);
又$|{\overrightarrow{BC}-\overrightarrow{BA}}|=\sqrt{2}$,
∴${(\sqrt{2}cosθ-1)}^{2}$+${(\sqrt{2}sinθ-1)}^{2}$=2,
∴2-2$\sqrt{2}$(cosθ+sinθ)+2=2,
即sinθ+cosθ=$\frac{\sqrt{2}}{2}$,
两边平方得:1+2sinθcosθ=$\frac{1}{2}$,
化简得sin2θ=-$\frac{1}{2}$;
(2)∵$\overrightarrow{OC}$=($\sqrt{2}$cosθ,$\sqrt{2}$sinθ),$\overrightarrow{OA}$=(1,1),$\overrightarrow{OB}$=(1,-1),
且实数m,n满足$m\overrightarrow{OA}+n\overrightarrow{OB}=\overrightarrow{OC},θ∈({0,\frac{π}{2}})$,
∴m(1,1)+n(1,-1)=($\sqrt{2}$cosθ,$\sqrt{2}$sinθ),
即$\left\{\begin{array}{l}{m+n=\sqrt{2}cosθ}\\{m-n=\sqrt{2}sinθ}\end{array}\right.$,
解得m=$\frac{\sqrt{2}(sinθ+cosθ)}{2}$,n=$\frac{\sqrt{2}(cosθ-sinθ)}{2}$;
∴(m-3)2+n2=m2+n2-6m+9,
=-3$\sqrt{2}$(sinθ+cosθ)+10
=-6sin(θ+$\frac{π}{4}$)+10,
∴当sin(θ+$\frac{π}{4}$)=-1时,(m-3)2+n2取得最大值16.
点评 本题主要考查了向量的坐标计算、减法、模的坐标计算以及三角函数的化简求值问题,是综合性题目.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
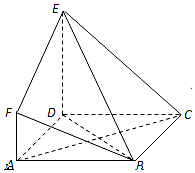 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,∠EBD=45°.
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,∠EBD=45°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{x}{2}$+$\frac{π}{6}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=sin(2x-$\frac{π}{6}$) | D. | y=cos(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊥α,α⊥β,m∥n⇒n∥β | B. | m∥α,α∩β=n⇒n∥m | ||
| C. | α∥β,m∥α,m⊥n,⇒n⊥β | D. | m⊥α,n⊥β,m∥n⇒α∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com