Question

已知直线y=ａx+1与双曲线３x²-y²=1交于A、B两点,(1)若以AB为直径的圆过坐标原点,求实数a的值;(2)是否存在这样的实数a,使A、B两点关于直线对称?若存在,请求出a的值;若不存在,请说明理由.

Answer 1

解:(1)由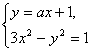消去y,得(3-a²)x²-2ax-2=0.①

依题意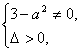

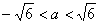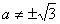即且.    ②

设A(x₁,y₁),B(x₂,y₂),

则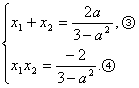

∵以AB为直径的圆过原点,∴OA⊥OB.

∴x₁x₂+y₁y₂=0.

但y₁y₂=a²x₁x₂+a(x₁+x₂)+1,

由③④,,.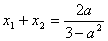

∴.

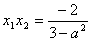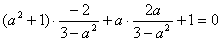解得a=±1且满足②.

(2)假设存在实数a,使A、B关于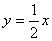对称,则直线y=ax+1与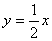垂直,

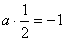∴a,即a=-2.

直线l的方程为y=-2x+1.

将a=-2代入③得x₁+x₂=４.

∴AB中点横坐标为2,

纵坐标为y=-2×2+1=-3.

但AB中点(2,-3)不在直线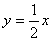上,

即不存在实数a,使A、B关于直线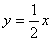对称.