
解:⊙A的方程可写为(x-1)2+(y-1)2=9,
⊙B的方程可写为(x+1)2+(y+1)2=4,
∴两圆心之间的距离满足3-2<|AB|=![]() =2
=2![]() <3+2,
<3+2,
即两圆心之间的距离小于两圆半径之和大于两圆半径之差.
∴两圆相交.
⊙A的方程与⊙B的方程左、右两边分别相减得-4x-4y-5=0,即4x+4y+5=0为过两圆交点的直线的方程.
设两交点分别为C、D,则CD:4x+4y+5=0.
点A到直线CD的距离为d=![]() =
=![]() .
.
由勾股定理,得|CD|=2![]() =2
=2![]() =
=![]() .
.
点评:判断两圆相交的方法,常用两圆心之间的距离d与两圆半径的和及差的绝对值比较大小,即当|R-r|<d<R+r时,两圆相交.求相交两圆的公共弦长及其方程一般不用求交点的方法,常用两方程相减法消去二次项得公共弦的方程,然后用勾股定理求弦长.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
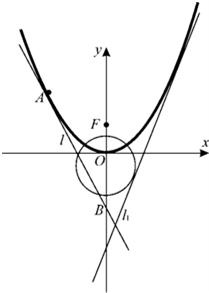 已知抛物线C1的方程为y=ax2(a>0),圆C2的方程为x2+(y+1)2=5,直线l1:y=2x+m(m<0)是C1、C2的公切线.F是C1的焦点.
已知抛物线C1的方程为y=ax2(a>0),圆C2的方程为x2+(y+1)2=5,直线l1:y=2x+m(m<0)是C1、C2的公切线.F是C1的焦点.| FM |
| FA |
| FB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com