
已知y=f(x)是定义在区间(-∞,0)∪(0,+∞)上的奇函数,且在(0,+∞)上是增函数,f(1)=0.
(1)解不等式f(x)≥0;
(2)设函数g(x)=-x2+mx-2m(x∈[0,1],m∈R),集合M={m|g(x)<0},集合N={m|f[g(x)]<0},求M∩N.
|
解:(1)因为f(x)为定义在区间(-∞,0)∪(0,+∞)上的奇函数且f(1)=0,所以f(-x)=-f(x),则f(-1)=-f(1)=0; 当x∈(0,+∞)时,因为f(x)在(0,+∞)上是增函数,由f(x)≥0得x≥1; 因为奇函数在关于原点对称的区间上单调性相同,又f(x)在(0,+∞)上是增函数,所以f(x)在区间(-∞,0)上也是增函数,又因为f(-1)=0,所以当x∈(-∞,0)时,由f(x)≥0得-1≤x<0. 综上所述,不等式f(x)≥0的解集为[-1,0)∪[1,+∞). (2)由(1)可知f(x)≥0的解集为[-1,0)∪[1,+∞),因为f(x)的定义域为(-∞,0)∪(0,+∞),所以f(x)<0的解集为(-∞,-1)∪(0,1).所以由f[g(x)]<0得g(x)<-1或0<g(x)<1,即N={m|g(x)<-1或0<g(x)<1},因为M={m|g(x)<0},所以M∩N={m|g(x)<-1}.因为g(x)=-x2+mx-2m(x∈[0,1]),所以g(x)<-1化为-x2+mx-2m+1<0,即(x-2)m+1-x2<0,因为x∈[0,1],所以m> 点评:本题所给函数是抽象函数,具有一定的综合性;在解决第一问时可以借助函数的单调性与奇偶性画出草图来帮助我们解题;在解决第二问时,可能有学生会分别求出集合M与N,然后再取交集,教师应该引导学生按照以上解答过程来解决省时省力. |
|
本题中的函数f(x)是抽象函数,因此只能由函数的性质,结合函数的草图来解决本题. |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:高三数学教学与测试 题型:044
已知曲线C的方程是(t+1) +2at)x+3at+b=0,直线l的
+2at)x+3at+b=0,直线l的
方程是y=t(x-1),若对任意实数t,曲线C恒过定点P(1,0).
(1)求定值a,b;
(2)直线l截曲线C所得弦长为d,记f(t)= ,则当t为何值时,f(t)有最大值,最大值是多少?
,则当t为何值时,f(t)有最大值,最大值是多少?
(3)若点M( )在曲线C上,又在直线l上,求
)在曲线C上,又在直线l上,求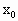 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:044
已知:如图射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.

(Ⅰ)当k为定值时,动点P的纵坐标y是其横坐标x的函数,求这个函数y=f(x)的解析式;
(Ⅱ)根据k的取值范围,确定y=f(x)的定义域.
查看答案和解析>>
科目:高中数学 来源:宁夏银川二中2011届高三第一次月考数学理科试题 题型:022
已知函数y=f(x)是偶函数,y=g(x)是奇函数,它们的定域[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式![]() <0的解集是________.
<0的解集是________.

查看答案和解析>>
科目:高中数学 来源:2012高三数学一轮复习单元练习题 函数与数列(2) 题型:044
已知f(x)=![]() (x∈R),P1(x1,y1)、P2(x2,y2)是函数y=f(x)图象上两点,且线段P1P2中点P的横坐标是
(x∈R),P1(x1,y1)、P2(x2,y2)是函数y=f(x)图象上两点,且线段P1P2中点P的横坐标是![]() .
.
(1)求证:点P的纵坐标是定值;
(2)若数列{an}的通项公式是an=f(![]() )(m∈N*,n=1,2,…m),求数列{an}的前m项和Sm;
)(m∈N*,n=1,2,…m),求数列{an}的前m项和Sm;
(3)在(2)的条件下,若m∈N*时,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:湖北省武汉二中08-09学年高二下学期期末考试(理) 题型:填空题
已知命题:
①函数f(x)=在(0, +∞)上是减函数;
②函数f(x)的定义域为R, 是x=x0为极值点的既不充分也不必要条件;
是x=x0为极值点的既不充分也不必要条件;
③y=f(x-2)的图象和y=f(2-x)的图象关于x=2对称
④在平面内, 到定点(2,1)的距离与定直线3x+4y-10=0的距离相等的点的轨迹是抛物线;
⑤若 , 则
, 则 (其中
(其中 );
);
其中, 正确命题的序号是 .(把你认为正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com