
【题目】已知函数![]() ,且存在不同的实数x1,x2,x3,使得f(x1)=f(x2)=f(x3),则x1x2x3的取值范围是( )
,且存在不同的实数x1,x2,x3,使得f(x1)=f(x2)=f(x3),则x1x2x3的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
作出y=f(x)的函数图象,设x1<x2<x3,f(x1)=f(x2)=f(x3)=t,1<t<2,求得x1,x2,x3,构造函数g(t)=(t﹣1)(2+log2t),1<t<2,求得导数,判断单调性,即可得到所求范围.
函数![]() 的图象如图所示:
的图象如图所示:
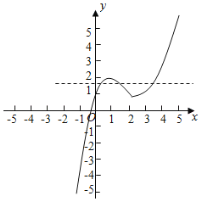
设x1<x2<x3,
又当x∈[2,+∞)时,f(x)=2x﹣2是增函数,
当x=3时,f(x)=2,
设f(x1)=f(x2)=f(x3)=t,1<t<2,
即有﹣x12+2x1+1=﹣x22+2x2+1=![]() t,
t,
故x1x2x3=(1![]() )(1
)(1![]() )(2+log2t)
)(2+log2t)
=(t﹣1)(2+log2t),
由g(t)=(t﹣1)(2+log2t),1<t<2,
可得g′(t)=2+log2t![]() 0,即g(t)在(1,2)递增,又g(1)=0,g(2)=3,
0,即g(t)在(1,2)递增,又g(1)=0,g(2)=3,
可得g(t)的范围是(0,3).
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中错误的是![]()
![]()
A. 若命题![]() 为真命题, 命题
为真命题, 命题![]() 为假命题, 则命题“
为假命题, 则命题“![]() ”为真命题
”为真命题
B. 命题“若![]() ,则
,则![]() 或
或![]() ”为真命题
”为真命题
C. 对于命题![]() ,
,![]() ,则
,则![]() ,
,![]()
D. “![]() ”是“
”是“![]() ”的充分不必要条件个
”的充分不必要条件个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现行的个税法修正案规定:个税免征额由原来的2000元提高到3500元,并给出了新的个人所得税税率表:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3% |
超过1500元至4500元的部分 | 10% |
超过4500元至9000元的部分 | 20% |
超过9000元至35000元的部分 | 25% |
…… | … |
例如某人的月工资收入为5000元,那么他应纳个人所得税为:![]() (元).
(元).
(Ⅰ)若甲的月工资收入为6000元,求甲应纳的个人收的税;
(Ⅱ)设乙的月工资收入为![]() 元,应纳个人所得税为
元,应纳个人所得税为![]() 元,求
元,求![]() 关于
关于![]() 的函数;
的函数;
(Ⅲ)若丙某月应纳的个人所得税为1000元,给出丙的月工资收入.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在二项式![]() 的展开式中,
的展开式中,
(1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(最后结果用算式表达,不用计算出数值)
(2)若展开式前三项的二项式系数的和等于79,求展开式中系数最大的项.(最后结果用算式表达,不用计算出数值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号,某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式: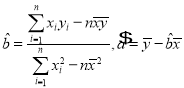 ;参考数据:
;参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛.若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() 各局比赛结果相互独立.则甲在4局以内(含4局)赢得比赛的概率为( )
各局比赛结果相互独立.则甲在4局以内(含4局)赢得比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水果的价格会受到需求量和天气的影响.某采购员定期向某批发商购进某种水果,每箱水果的价格会在当日市场价的基础上进行优惠,购买量越大优惠幅度越大,采购员通过对以往的10组数据进行研究,发现可采用![]() 来作为价格的优惠部分
来作为价格的优惠部分![]() (单位:元/箱)与购买量
(单位:元/箱)与购买量![]() (单位:箱)之间的回归方程,整理相关数据得到下表(表中
(单位:箱)之间的回归方程,整理相关数据得到下表(表中![]() ):
):
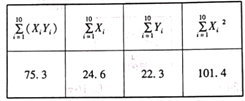
(1)根据参考数据,
①建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②若当日该种水果的市场价为200元/箱,估算购买100箱该种水果所需的金额(精确到0.1元).
(2)在样本中任取一点,若它在回归曲线上或上方,则称该点为高效点.已知这10个样本点中,高效点有4个,现从这10个点中任取3个点,设取到高效点的个数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为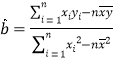 ,
,![]() ,参考数据:
,参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com