
【题目】
已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是![]() ,双曲线过点
,双曲线过点![]()
(1)求双曲线方程
(2)动直线![]() 经过
经过![]() 的重心G,与双曲线交于不同的两点M、N,问:是否存在直线
的重心G,与双曲线交于不同的两点M、N,问:是否存在直线![]() ,使G平分线段MN,证明你的结论
,使G平分线段MN,证明你的结论
【答案】(1)所求双曲线方程为![]() ="1" ;
="1" ;
(2)所求直线![]() 不存在.
不存在.
【解析】
本试题主要是考查了双曲线方程的求解,已知直线与双曲线的位置关系的综合运用.
(1)利用已知中的渐近线方程是![]() ,双曲线过点
,双曲线过点![]()
那么设出双曲线的标准方程,然后代入点和a,b的关系得到求解.
(2)假设存在直线![]() ,使G(2,2)平分线段MN,那么利用对称性,分别设出点的坐标,那么联立方程组,可知斜率,得到直线的方程,从而验证是否存在.
,使G(2,2)平分线段MN,那么利用对称性,分别设出点的坐标,那么联立方程组,可知斜率,得到直线的方程,从而验证是否存在.
(1)如图,设双曲线方程为![]() =1 …………1分
=1 …………1分

由已知得 ………………………………………3分
………………………………………3分
解得![]() …………………………………………………5分
…………………………………………………5分
所以所求双曲线方程为![]() ="1" ……………………6分
="1" ……………………6分
(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)…………………………………………………………8分
假设存在直线![]() ,使G(2,2)平分线段MN,
,使G(2,2)平分线段MN,
设M(x1,y1),N(x2,y2) 则有
![]() ,∴kl=
,∴kl=![]() ……………………10分
……………………10分
∴l的方程为y=![]() (x-2)+2,12分
(x-2)+2,12分
由 ,消去y,整理得x2-4x+28="0"
,消去y,整理得x2-4x+28="0"
∵Δ=16-4×28<0,∴所求直线![]() 不存在…………………………………………14分
不存在…………………………………………14分


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
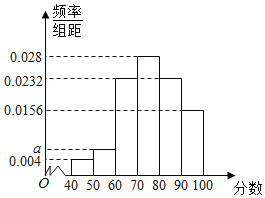
(1)求频率分布直方图中a的值;
(2)求这50名问卷评分数据的中位数;
(3)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,焦距为6.
,焦距为6.
(1)求椭圆![]() 的方程.
的方程.
(2)过椭圆左顶点的两条斜率之积为![]() 的直线分别与椭圆交于
的直线分别与椭圆交于![]() 点.试问直线
点.试问直线![]() 是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?说明理由.
垂直?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕头某家电企业要将刚刚生产的100台变频空调送往市内某商场,现有4辆甲型货车和8辆乙型货车可供调配,每辆甲型货车的运输费用是400元,可装空调20台,每辆乙型货车的运输费用是300元,可装空调10台,若每辆车至多运一次,则企业所花的最少运费为( )
A. 2000元B. 2200元C. 2400元D. 2800元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率
)的离心率![]() ,直线
,直线![]() 被以椭圆
被以椭圆![]() 的短轴为直径的圆截得的弦长为
的短轴为直径的圆截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两个不同的点,且
两个不同的点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ',
',![]() 时,
时,![]()
![]() (其中
(其中![]() 表示
表示![]() ,
,![]() ,…,
,…,![]() 中的最大项),有以下结论:
中的最大项),有以下结论:
① 若数列![]() 是常数列,则
是常数列,则![]() ;
;
② 若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
③ 若数列![]() 是公比为
是公比为![]() 的等比数列,则
的等比数列,则![]() :
:
④ 若存在正整数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则
,则![]() ,是数列
,是数列![]() 的最大项.
的最大项.
其中正确结论的序号是____(写出所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com