
【题目】从某学校高三年级共800名男生中随机抽取50名学生作为样本测量身高.测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组![]() ;第二组
;第二组![]() ;…;第八组
;…;第八组![]() .下图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组与第八组人数之和为第七组的两倍.
.下图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组与第八组人数之和为第七组的两倍.
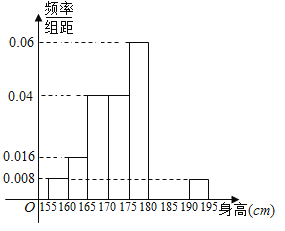
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)求第六组和第七组的频率并补充完整频率分布直方图.
【答案】(1)144人(2)频率分别为0.08和0.06,见解析
【解析】
(1)由直方图求出前五组频率为0.82,后三组频率为![]() ,由此能求出这所学校高三男生身高在
,由此能求出这所学校高三男生身高在![]() 以上(含
以上(含![]() 的人数.
的人数.
(2)由频率分布直方图得第八组频率为0.04,人数为2人,设第六组人数为![]() ,则第七组人数为
,则第七组人数为![]() ,再由
,再由![]() ,得
,得![]() ,即第六组人数为4人,第七组人数为3人,频率分别为0.08,0.06.由此能求出结果.
,即第六组人数为4人,第七组人数为3人,频率分别为0.08,0.06.由此能求出结果.
(1)由图知前5组频率为![]()
![]() 后三组频率为
后三组频率为![]() .
.
![]() 全校高三男生身高在180cm以上的人有
全校高三男生身高在180cm以上的人有![]() 人.
人.
(2)如图知第八组频率为![]() ,人数为
,人数为![]() 人.
人.
设第六组人数为m,后三组共9人.
![]() 第七组人数为
第七组人数为![]() .
.
![]() ,
,![]() .
.
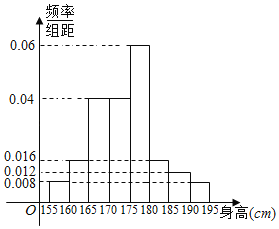
即第六组4人,第七组3人,其频率分别为0.08和0.06,高度分别为0.016和0.012,如图所示.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=2an﹣2(n∈N*),数列{bn}满足bn=(2n﹣1)an,数列{bn}的前n项和Tn(n∈N*),
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和Tn;
(3)求![]() 的最小值以及取得最小值时n的值.
的最小值以及取得最小值时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型企业针对改善员工福利的![]() ,
,![]() ,
,![]() 三种方案进行了问卷调查,调查结果如下:
三种方案进行了问卷调查,调查结果如下:
支持 | 支持 | 支持 | |
35岁以下的人数 | 200 | 400 | 800 |
35岁及以上的人数 | 100 | 100 | 400 |
(1)从所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,已知从支持
人,已知从支持![]() 方案的人中抽取了6人,求
方案的人中抽取了6人,求![]() 的值.
的值.
(2)从支持![]() 方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 、
、![]() 的值和
的值和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上有且只有两个不同零点,求实数
上有且只有两个不同零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对平面区域![]() ,用
,用![]() 表示属于
表示属于![]() 的所有整点(即
的所有整点(即![]() 平面上坐标
平面上坐标![]() 都是整数的点)的个数.若
都是整数的点)的个数.若![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界);
所围成的区域(包括边界);![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界).则
所围成的区域(包括边界).则![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com