
 的x与y的部分对应值如下表:
的x与y的部分对应值如下表:| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 11 | | 1 | -1 | -1 | 1 | 5 |
 的两根分别为
的两根分别为 、
、 ,下面说法错误的是( ) .
,下面说法错误的是( ) . B.
B.
 时,
时, D.当
D.当 时,
时, 有最小值
有最小值科目:高中数学 来源:不详 题型:解答题
| | 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 |
| 使用淡化海砂 | 25 | 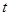 | 30 |
| 使用未经淡化海砂 |  | 15 | 30 |
| 总计 | 40 | 20 | 60 |
 ,
,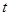 的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?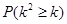 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ( )
( )A.当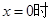 , , 的平均值 的平均值 |
B.当 变动一个单位时, 变动一个单位时, 的实际变动量 的实际变动量 |
C.当 变动一个单位时, 变动一个单位时, 的平均变动量 的平均变动量 |
D.当 变动一个单位时, 变动一个单位时, 的平均变动量 的平均变动量 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 、
、 、……
、…… 的平均值为
的平均值为 ,方差为
,方差为 ,则
,则 ,
, ,……
,……  的平均值和方差分别为( )
的平均值和方差分别为( )A. 和 和 | B.3 +5和9 +5和9 |
C.3 +5和 +5和 | D.3 +5 和9 +5 和9 +30 +30 +25 +25 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 所表示的直线必经过的点;
所表示的直线必经过的点; ;
; )
) 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 +2,
+2, +2, ,
+2, , +2的平均数为10,方差为3,则样本2
+2的平均数为10,方差为3,则样本2 +3,2
+3,2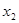 +3,… ,2
+3,… ,2 +3,
+3,A.19,12,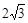 | B.23,12,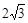 | C.23,18, | D.19,18, |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 [
[ | A.①②⑤③④ | B.③②④⑤① | C.②④③①⑤ | D.②⑤④③① |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 患慢性气管炎 | 未患慢性气管炎 | 总计 |
| 吸烟 | 360 | 320 | 680 |
| 不吸烟 | 140 | 180 | 320 |
| 合计 | 500 | 500 | 1000 |
 ,且P(K2≥6.635)≈0.01,)
,且P(K2≥6.635)≈0.01,)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com