
【题目】已知命题p:若x>0,则函数y=x+ ![]() 的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q)
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=2BB1=2BC,E为D1C1的中点,连结ED,EC,EB和DB.
(Ⅰ)证明:A1D1∥平面EBC;
(Ⅱ)证明:平面EDB⊥平面EBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个路口的红绿灯,红灯亮的时间为40秒,黄灯亮的时间为5秒,绿灯亮的时间为50秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?
(1)红灯;
(2)黄灯;
(3)不是红灯.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D是以点A(4,1),B(﹣1,﹣6),C(﹣2,3)为顶点的三角形区域(包括边界及内部).
(1)写出表示区域D的不等式组;
(2)设点B(﹣1,﹣6)、C(﹣2,3)在直线4x﹣3y﹣a=0的异侧,求a的取值范围;
(3)若目标函数z=kx+y(k<0)的最小值为﹣k﹣6,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:
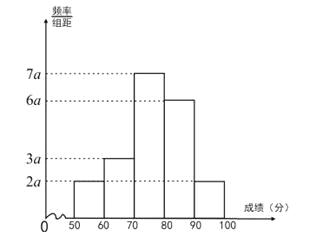
(Ⅰ)求频率分布直方图中![]() 的值;
的值;
(Ⅱ)分别求出成绩落在![]() ,
, ![]() 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
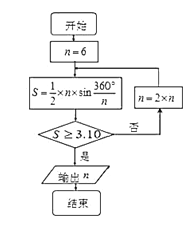
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com