
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 关于坐标轴对称,以坐标原点
关于坐标轴对称,以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系, ![]() ,
, ![]() 为椭圆
为椭圆![]() 上两点.
上两点.
(1)求直线![]() 的直角坐标方程与椭圆
的直角坐标方程与椭圆![]() 的参数方程;
的参数方程;
(2)若点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 在第一象限内,求四边形
在第一象限内,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
【答案】(1)直角方程![]() 参数方程为
参数方程为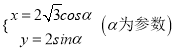 (2)6.
(2)6.
【解析】试题分析:
(1)将点A的坐标化为直角坐标便可得到直线![]() 的倾斜角,进而可得直线的方程;然后根据待定系数法可得椭圆的直角坐标方程,再化为参数方程即可.(2)由(1)可得点M(2
的倾斜角,进而可得直线的方程;然后根据待定系数法可得椭圆的直角坐标方程,再化为参数方程即可.(2)由(1)可得点M(2![]() cosα,2sinα) ,0<α<
cosα,2sinα) ,0<α<![]() ,进而可得点M到直线OA的距离d,所以S=S△MOA+S△MOB
,进而可得点M到直线OA的距离d,所以S=S△MOA+S△MOB
=6sin(α+![]() ),结合三角知识可得结果.
),结合三角知识可得结果.
试题解析:
(1)由A(![]() ,
,![]() )得直线OA的倾斜角为
)得直线OA的倾斜角为![]() ,
,
所以直线OA斜率为tan![]() =-1,
=-1,
故直线OA的方程为![]() ,即x+y=0.
,即x+y=0.
由x=ρcosα,y=ρsinα可得点A的直角坐标为(-![]() ,
, ![]() ),
),
因为椭圆C关于坐标轴对称,且B(2![]() ,0),
,0),
所以可设椭圆C:![]() +
+![]() =1,其中t>0且t≠12,
=1,其中t>0且t≠12,
将(-![]() ,
, ![]() )的坐标代入曲线C的方程,可得t=4,
)的坐标代入曲线C的方程,可得t=4,
故椭圆C的方程为![]() ,
,
所以椭圆C的参数方程为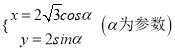 .
.
(2)由(1)得M(2![]() cosα,2sinα),0<α<
cosα,2sinα),0<α<![]() .
.
点M到直线OA的距离d=![]() cosα+
cosα+![]() sinα.
sinα.
所以S=S△MOA+S△MOB=(3cosα+![]() sinα)+2
sinα)+2![]() sinα=3cosα+3
sinα=3cosα+3![]() sinα=6sin(α+
sinα=6sin(α+![]() ),
),
故当α=![]() 时,四边形OAMB面积S取得最大值6.
时,四边形OAMB面积S取得最大值6.


科目:高中数学 来源: 题型:
【题目】在![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 取最大值,且
取最大值,且![]() 的周长为
的周长为![]() 时,求
时,求![]() 面积的最大值,并指出面积取最大值时
面积的最大值,并指出面积取最大值时![]() 的形状.(参考知识:已知
的形状.(参考知识:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出100户调查社会购买力的某一项指标,应采用的最佳抽样方法是分层抽样
②线性回归直线![]() 一定过样本中心点
一定过样本中心点![]()
③对于一组数据![]() ,如果将它们改变为
,如果将它们改变为![]() ,则平均数与方差均发生变化
,则平均数与方差均发生变化
④若一组数据1、![]() 、2、3的众数是2,则这组数据的中位数是2
、2、3的众数是2,则这组数据的中位数是2
⑤用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为76
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 是定义在
是定义在![]() 上的不恒为零的函数,对于任意实数
上的不恒为零的函数,对于任意实数![]() 满足:
满足: ![]() ,
,![]()
![]() ,
,![]() 考查下列结论:①
考查下列结论:①![]() ;②
;②![]() 为奇函数;③数列
为奇函数;③数列![]() 为等差数列;④数列
为等差数列;④数列![]() 为等比数列.
为等比数列.
以上结论正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=![]() ,AD=2,PA=PD=
,AD=2,PA=PD=![]() ,E,F分别是棱AD,PC的中点.
,E,F分别是棱AD,PC的中点.

(1)证明:EF∥平面PAB;
(2)若二面角P-AD-B为60°.
①证明:平面PBC⊥平面ABCD;
②求直线EF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 满足如下条件:
满足如下条件:
①函数![]() 的最小值为
的最小值为![]() ,最大值为9;
,最大值为9;
②![]() 且
且![]() ;
;
③若函数![]() 在区间
在区间![]() 上是单调函数,则
上是单调函数,则![]() 的最大值为2.
的最大值为2.
试探究并解决如下问题:
(Ⅰ)求![]() ,并求
,并求![]() 的值;
的值;
(Ⅱ)求函数![]() 的图象的对称轴方程;
的图象的对称轴方程;
(Ⅲ)设![]() 是函数
是函数![]() 的零点,求
的零点,求![]() 的值的集合.
的值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知向量![]() ,
,![]() ,函数
,函数![]() ,若
,若![]() 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为![]() ,且图象过点
,且图象过点![]() .
.
(1)求![]() 表达式和
表达式和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .以
.以![]() 为顶点,
为顶点,![]() 分别为左、右焦点的椭圆
分别为左、右焦点的椭圆![]() ,恰好经过点
,恰好经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com