
【题目】某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.

(1)若蛋糕店一天制作17个生日蛋糕,
①求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
②在当天的利润不低于750元的条件下,求当天需求量不低于18个的概率.
(2)若蛋糕店计划一天制作16个或17个生日蛋糕,请你以蛋糕店一天利润的期望值为决定依据,判断应该制作16个是17个?
【答案】(1)①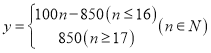 ;②
;②![]() ;
;
(2)一天应该制作![]() 个生日蛋糕.
个生日蛋糕.
【解析】
试题分析:(1)①由题意得,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,即可求解函数的解析式;②根据当天的利润不低于750元为事件
,即可求解函数的解析式;②根据当天的利润不低于750元为事件![]() ,设当天需求量不低于18个为事件
,设当天需求量不低于18个为事件![]() ,利用条件概率的计算公式,即可求解概率;(2)分别求出一天制作
,利用条件概率的计算公式,即可求解概率;(2)分别求出一天制作![]() 和
和![]() 个,列出相应的分布列,求解数学期望,即可作出选择.
个,列出相应的分布列,求解数学期望,即可作出选择.
试题解析:(1)①当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
得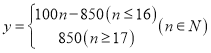 .
.
②设当天的利润不低于750元为事件![]() ,设当天需求量不低于18个为事件
,设当天需求量不低于18个为事件![]() ,
,
由①得“利润不低于![]() 元”等价于“需求量不低于16个”,则
元”等价于“需求量不低于16个”,则![]() ,
,
![]()
(2)蛋糕店一天应制作17个生日蛋糕,理由如下:
若蛋糕店一天制作17个,![]() 表示当天的利润(单位:元),
表示当天的利润(单位:元),![]() 的分布列为
的分布列为
| 550 | 650 | 750 | 850 |
| 0.1 | 0.2 | 0.16 | 0.54 |
![]()
若蛋糕店一天制作16个,![]() 表示当天的利润(单位:元),
表示当天的利润(单位:元),![]() 的分布列为
的分布列为
| 600 | 700 | 800 |
| 0.1 | 0.2 | 0.7 |
![]() ,
,
由以上的计算结果可以看出,![]() ,即一天制作17个的利润大于制作16个的利润,
,即一天制作17个的利润大于制作16个的利润,
所以蛋糕店一天应该制作17个生日蛋糕


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA![]() =4,点D是AB的中点
=4,点D是AB的中点

(1)求证:AC![]() BC
BC![]() ;
;
(2)求证:AC![]() //平面CDB
//平面CDB![]() ;
;
(3)求二面角B-DC-B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
将圆![]() 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线![]() .
.
(1)写出曲线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别为曲线
分别为曲线![]() 和直线
和直线![]() 上的一点,求
上的一点,求![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com