
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x(年) | 3 | 5 | 6 | 7 | 9 |
| 推销金额y(万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
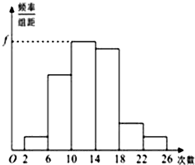 为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如表的频率分布表与如图直方图:
为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如表的频率分布表与如图直方图:| 组别 | 锻炼次数 | 频数(人) | 频率 |
| 1 | [2,6) | 2 | 0.04 |
| 2 | [6,10) | 11 | 0.22 |
| 3 | [10,14) | 16 | c |
| 4 | [14,18) | 15 | 0.30 |
| 5 | [18,22) | d | e |
| 6 | [22,26] | 2 | 0.04 |
| 合计 | M | 1.00 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
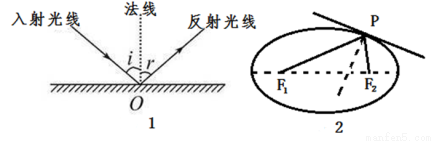
阅读下列有关光线的入射与反射的两个事实现象,现象(1):光线经平面镜反射满足入射角 与反射角
与反射角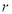 相等(如图1);现象(2):光线从椭圆的一个焦点出发经椭圆反射后通过另一个焦点(如图2).试结合上述事实现象完成下列问题:
相等(如图1);现象(2):光线从椭圆的一个焦点出发经椭圆反射后通过另一个焦点(如图2).试结合上述事实现象完成下列问题:
(1)有一椭圆型台球桌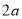 ,长轴长为短轴长为
,长轴长为短轴长为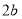 .将一放置于焦点处的桌球击出,经过球桌边缘的反射(假设球的反射完全符合现象(2))后第一次返回到该焦点时所经过的路程记为
.将一放置于焦点处的桌球击出,经过球桌边缘的反射(假设球的反射完全符合现象(2))后第一次返回到该焦点时所经过的路程记为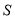 ,求
,求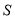 的值(用
的值(用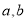 表示);
表示);
(2)结论:椭圆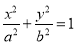 上任一点
上任一点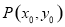 处的切线
处的切线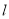 的方程为
的方程为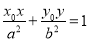 .记椭圆
.记椭圆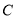 的方程为
的方程为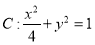 .
.
①过椭圆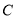 的右准线上任一点
的右准线上任一点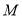 向椭圆
向椭圆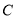 引切线,切点分别为
引切线,切点分别为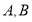 ,求证:直线
,求证:直线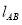 恒过一定点;
恒过一定点;
②设点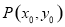 为椭圆
为椭圆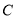 上位于第一象限内的动点,
上位于第一象限内的动点,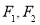 为椭圆
为椭圆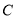 的左右焦点,点
的左右焦点,点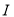 为
为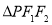 的内心,直线
的内心,直线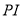 与
与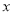 轴相交于点
轴相交于点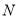 ,求点
,求点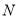 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{10}$) | B. | (1,$\sqrt{3}$) | C. | (1,3) | D. | (1,10) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com