练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】《九章算术》是中国古代第一部数学专著，全书总结了战国、秦、汉时期的数学成就。“更相减损术”便出自其中，原文记载如下：“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。”其核心思想编译成如示框图，若输入的，分别为45，63，则输出的为（ ）

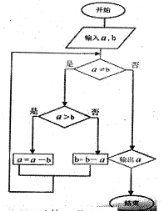
    A. 2B. 3C. 5D. 9

    【答案】D

    【解析】

    通过已知，可以判断这是在求两数的最大公约数。也可以按照循环结构的特点，先判断后执行，分别求出当前的值，直到循环结束。

    通过阅读可以知道，这是利用更相减损术求45，63的最大公约数，63，45的最大公约数是9。也可以按照循环结构来求解，如下表：

    循环次数

    a

    b

    初始

    45

    63

    第一次

    45

    18

    第二次

    27

    18

    第三次

    9

    18

    第四次

    9

    9

    第五次

    输出a=9

    因此本题选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆锥的侧面展开图是一个半圆．

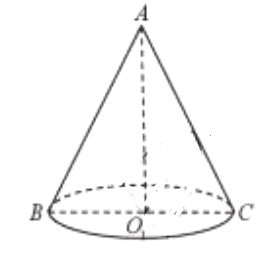
    （1）求圆锥的母线与底面所成的角；

    （2）过底面中心且平行于母线的截平面，若截面与圆锥侧面的交线是焦参数（焦点到准线的距离）为的抛物线，求圆锥的全面积；

    （3）过底面点作垂直且于母线的截面，若截面与圆锥侧面的交线是长轴为的椭圆，求椭圆的面积（椭圆号的面积）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划．2018年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本2500万元，每生产x（百辆），需另投入成本万元，且．由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完．

    （1）求出2018年的利润L（x）（万元）关于年产量x（百辆）的函数关系式；（利润=销售额-成本）

    （2）2018年产量为多少百辆时，企业所获利润最大?并求出最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数

    讨论的单调性；

    若是的极值点，且曲线在两点 处的切线相互平行，这两条切线在轴上的截距分别为，求的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂有两个车间生产同一种产品，第一车间有工人200人，第二车间有工人400人，为比较两个车间工人的生产效率，采用分层抽样的方法抽取工人，并对他们中每位工人生产完成一件产品的时间（单位：min）分别进行统计，得到下列统计图表（按照[55，65），[65，75），[75，85），[85，95]分组）．

    分组

    频数

    [55，65）

    2

    [65，75）

    4

    [75，85）

    10

    [85，95]

    4

    合计

    20

    第一车间样本频数分布表

    （Ⅰ）分别估计两个车间工人中，生产一件产品时间小于75min的人数；

    （Ⅱ）分别估计两车间工人生产时间的平均值，并推测哪个车间工人的生产效率更高？（同一组中的数据以这组数据所在区间中点的值作代表）

    （Ⅲ）从第一车间被统计的生产时间小于75min的工人中，随机抽取3人，记抽取的生产时间小于65min的工人人数为随机变量X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆的方程为：，为圆上任意一点，过作轴的垂线，垂足为，点在上，且.

    （1）求点的轨迹的方程；

    （2）过点的直线与曲线交于、两点，点的坐标为，的面积为，求的最大值，及直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在上的奇函数，当时，，给出下列命题：

    ①当时， ②函数有3个零点

    ③的解集为 ④，都有

    其中正确命题的个数是（ ）

    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆O经过椭圆C：=1（a＞b＞0）的两个焦点以及两个顶点，且点（b，）在椭圆C上．

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）若直线l与圆O相切，与椭圆C交于M、N两点，且|MN|=，求直线l的倾斜角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某校举行的航天知识竞赛中，参与竞赛的文科生与理科生人数之比为，且成绩分布在，分数在以上（含）的同学获奖. 按文理科用分层抽样的方法抽取人的成绩作为样本，得到成绩的频率分布直方图（见下图）.

    （1）求的值，并计算所抽取样本的平均值（同一组中的数据用该组区间的中点值作代表）；

    （2）填写下面的列联表，能否有超过的把握认为“获奖与学生的文理科有关”？

    文科生

    理科生

    合计

    获奖

    不获奖

    合计

    附表及公式：

    ，其中

    查看答案和解析>>

    同步练习册答案