
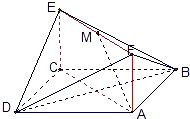
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=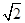 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.

(Ⅰ)求证AM//平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(Ⅲ)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
(1)对于线面平行的证明,主要是分析借助于中位线来得到AM∥OE
(2)60º(3)P是AC的中点
【解析】
试题分析:解法一: (1)记AC与BD的交点为O,连接OE, ∵O、M分别是AC、EF的中点, ACEF是矩形,∴四边形AOEM是平行四边形,
∴AM∥OE.∵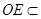 平面BDE,
平面BDE,
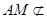 平面BDE,∴AM∥平面BDE.……4分
平面BDE,∴AM∥平面BDE.……4分
(2)在平面AFD中过A作AS⊥DF于S,连结BS,∵AB⊥AF, AB⊥AD,
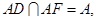 ∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF.∴∠BSA是二面角A—DF—B的平面角.
在RtΔASB中,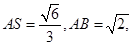
∴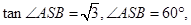 ∴二面角A—DF—B的大小为60º.……8分
∴二面角A—DF—B的大小为60º.……8分
(3)设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,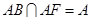 ,∴PQ⊥平面ABF,
,∴PQ⊥平面ABF, 平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
∵ΔPAQ为等腰直角三角形,∴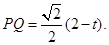 又∵ΔPAF为直角三
又∵ΔPAF为直角三
角形,∴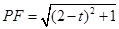 ,∴
,∴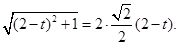 所以t=1或t=3(舍去),即点P是AC的中点.……12分
所以t=1或t=3(舍去),即点P是AC的中点.……12分
解法二: (1)建立空间直角坐标系.
设 ,连接NE,
则点N、E的坐标分别是(
,连接NE,
则点N、E的坐标分别是( 、(0,0,1),
、(0,0,1),
∴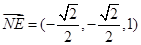 , 又点A、M的坐标分别是
, 又点A、M的坐标分别是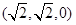 ,(
,(
∴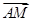 =(
=(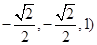 ∴
∴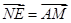 且NE与AM不共线,∴NE∥AM.又∵
且NE与AM不共线,∴NE∥AM.又∵ 平面BDE,
平面BDE,
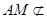 平面BDE,∴AM∥平面BDE.
平面BDE,∴AM∥平面BDE.
(2)∵AF⊥AB,AB⊥AD,AF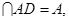 ∴AB⊥平面ADF.
∴AB⊥平面ADF.
∴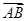
 为平面DAF的法向量.
为平面DAF的法向量.
∵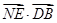 =(
=(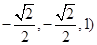 ·
· =0,
=0,
∴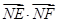 =(
=(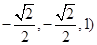 ·
·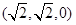 =0得
=0得
 ,
,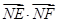 ,∴NE为平面BDF的法向量.
,∴NE为平面BDF的法向量.
∴cos<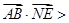 =
=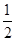 ∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
(3)设P(t,t,0)(0≤t≤ )得
)得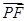
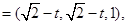 ∴
∴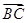 =(0,
=(0,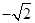 , 0)
, 0)
又∵PF和BC所成的角是60º.∴
解得 或
或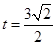 (舍去),即点P是AC的中点.
(舍去),即点P是AC的中点.
考点:空间中线面的位置关系
点评:解决的关键是根据线面平行的判定定理,以及空间的法向量来求解二面角的平面角的大小,属于中档题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=| 2 |
| 2 |
| ME |
| FM |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.| 2 |
| 5 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com