练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

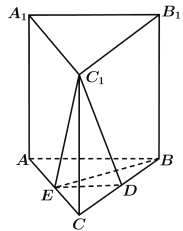
    【题目】如图，在直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．

    求证：（1）A1B1∥平面DEC1；

    （2）BE⊥C1E．

    【答案】（1）见解析；（2）见解析.

    【解析】

    (1)由题意结合几何体的空间结构特征和线面平行的判定定理即可证得题中的结论；

    (2)由题意首先证得线面垂直，然后结合线面垂直证明线线垂直即可.

    （1）因为D，E分别为BC，AC的中点，

    所以ED∥AB.

    在直三棱柱ABC-A1B1C1中，AB∥A1B1，

    所以A1B1∥ED.

    又因为ED平面DEC1，A1B1平面DEC1，

    所以A1B1∥平面DEC1.

    （2）因为AB=BC，E为AC的中点，所以BE⊥AC.

    因为三棱柱ABC-A1B1C1是直棱柱，所以CC1⊥平面ABC.

    又因为BE平面ABC，所以CC1⊥BE.

    因为C1C平面A1ACC1，AC平面A1ACC1，C1C∩AC=C，

    所以BE⊥平面A1ACC1.

    因为C1E平面A1ACC1，所以BE⊥C1E.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列，，其前项和满足，其中.

    （1）设，证明：数列是等差数列；

    （2）设，为数列的前项和，求证：；

    （3）设（为非零整数，），试确定的值，使得对任意，都有成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【选修4-4：坐标系与参数方程】

    在平面直角坐标系中，曲线的参数方程为： （为参数， ），将曲线经过伸缩变换： 得到曲线.

    （1）以原点为极点， 轴的正半轴为极轴建立坐标系，求的极坐标方程；

    （2）若直线（为参数）与相交于两点，且，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若函数有两个零点，.

    （1）求实数的取值范围；

    （2）求证：当时，；

    （3）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正三棱柱（底面是正三角形，侧棱垂直底面）的各条棱长均相等，为的中点．、分别是、上的动点（含端点），且满足．当运动时，下列结论中正确的是______ (填上所有正确命题的序号)．

    ①平面平面；

    ②三棱锥的体积为定值；

    ③可能为直角三角形；

    ④平面与平面所成的锐二面角范围为．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数有两个零点．

    （1）若函数的两个零点是和，求的值，并写出不等式的解集；

    （2）当时，函数有两个零点和，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设a为实数，函数f(x)＝x2＋|x－a|＋1，x∈R.

    (1)讨论f(x)的奇偶性；

    (2)求f(x)的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数与听课时间（单位：分钟）之间的关系满足如图所示的图象，当 时，图象是二次函数图象的一部分，其中顶点，过点；当 时，图象是线段BC，其中．根据专家研究，当注意力指数大于62时，学习效果最佳．要使得学生学习效果最佳，则教师安排核心内容的时间段为____________.（写成区间形式）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的三边长分别为,,,M是AB边上的点,P是平面ABC外一点.给出下列四个命题：①若平面ABC,则三棱锥的四个面都是直角三角形；②若平面ABC,且M是边AB的中点,则有；③若,平面ABC,则面积的最小值为；④若,P在平面ABC上的射影是内切圆的圆心,则点P到平面ABC的距离为.其中正确命题的序号是________.（把你认为正确命题的序号都填上）

    查看答案和解析>>

    同步练习册答案