练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．设Sn为等差数列{an}的前n项和，若已知S6＜S7，S7＞S8，则下列叙述中正确的个数有（　　）
    ①S7是所有Sn（n∈N*）中的最大值；
    ②a7是所有an（n∈N*）中的最大值；
    ③公差d一定小于0；
    ④S9一定小于S6．
    A．1个B．2个C．3个D．4个

    分析 利用等差数列的性质求解．

    解答 解：∵a7＞0，a8＜0，∴S7最大，故①正确；
    ∵d＜0，∴a1最大，故②错误；
    由s6＜s7，S7＞S8可得S7-S6=a7＞0，S8-S7=a8＜0
    ∴a8-a7=d＜0，故③正确；
    S9-S6=a7+a8+a9=3a8＜0，故④正确．
    故选：C．

    点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

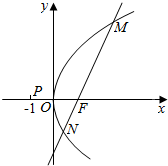    3．已知点F为抛物线C：y2=2px（p＞0）的焦点，过点F的动直线l与抛物线C交于M，N两点，如图．当直线l与x轴垂直时，|MN|=4．
    （Ⅰ）求抛物线C的方程；
    （Ⅱ）已知点P（-1，0），设直线PM的斜率为k1，直线PN的斜率为k2．请判断k1+k2是否为定值，若是，写出这个定值，并证明你的结论；若不是，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知集合A={1，2，3}，B={2，3，4，5}，全集U={1，2，3，4，5，6}，则∁U（A∩B）=（　　）
    A．{2，3}B．{1，4，5}C．{1，4，5，6}D．{1，2，3，4，5}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

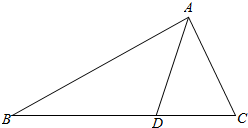    1．如图，在△ABC中，点D在BC边上，∠CAD=$\frac{π}{4}$，AC=$\frac{7}{2}$，cos∠ADB=-$\frac{{\sqrt{2}}}{10}$．
    （1）求sin∠C的值；
    （2）若BD=5，求△ABD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．在△ABC中，AB=AC，D为线段AC的中点，若BD的长为定值l，则△ABC面积的最大值为$\frac{2}{3}$$\sqrt{l}$（用l表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．下列说法中正确的是（　　）
    A．若a＞b，则ac2＞bc2
    B．若x≠0，则x+$\frac{4}{x}$的最小值为4
    C．“φ=$\frac{π}{2}$”是函数y=sin（x+φ）为偶函数“的充要条件
    D．命题“?x＞0，x-lnx＞0”的否定是“?x0＞0，x0-lnx0≤0”

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=sin（π-x）+$\sqrt{3}$cosx．
    （Ⅰ）求函数y=f（x）的最小周期；
    （Ⅱ）将函数y=f（x）的图象向右平移$\frac{π}{6}$个单位，得到函数y=g（x）的图象，求函数y=g（x）在区间[0，$\frac{5π}{6}$]上的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

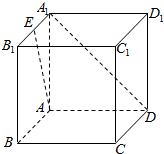    2．如图，在正方体ABCD-A1B1C1D1中，E为A1B1的中点，则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．给出命题：
    ①函数$y=cos（\frac{3}{2}x+\frac{π}{2}）$是奇函数；
    ②若α、β是第一象限角且α＜β，则tanα＜tanβ；
    ③$y=2sin\frac{3}{2}x$在区间$[-\frac{π}{3}，\frac{π}{2}]$上的最小值是-2，最大值是$\sqrt{2}$；
    ④$x=\frac{π}{8}$是函数$y=sin（2x+\frac{5}{4}π）$的一条对称轴．
    其中正确命题的序号是①④．

    查看答案和解析>>

    同步练习册答案