
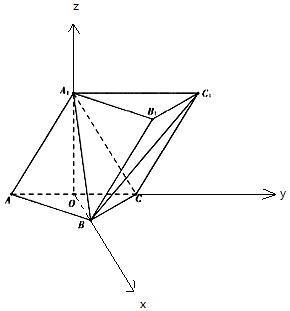
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面AA1C1C底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点. 
(Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求二面角A1﹣AB﹣C的余弦值.
【答案】证明:(Ⅰ)∵AA1=A1C,且O为AC的中点,∴A1O⊥AC,
又∵侧面AA1C1C⊥底面ABC,交线为AC,且A1O平面AA1C1C,
∴A1O⊥平面ABC.
解:(Ⅱ)以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
由已知可得O(0,0,0),A(0,﹣1,0), ![]() ,
, ![]()
∴ ![]() ,
, ![]() ,
,
设平面AA1B的一个法向量为 ![]() ,
,
则有  ,
,
令x=1,得 ![]() ,z=1
,z=1
∴ ![]() …(8分)
…(8分)
∵A1O⊥平面ABC
∴平面ABC的一个法向量 ![]()
∴ ![]()
又二面角A1﹣AB﹣C是锐角
∴二面角A1﹣AB﹣C的余弦值为 ![]()
【解析】(Ⅰ)推导出A1O⊥AC,由此利用侧面AA1C1C⊥底面ABC,能证明A1O⊥平面ABC.(Ⅱ)以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出二面角A1﹣AB﹣C的余弦值.
【考点精析】利用直线与平面垂直的判定对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】有以下判断: ①f(x)= ![]() 与g(x)=
与g(x)= ![]() 表示同一函数;
表示同一函数;
②函数y=f(x)的图象与直线x=1的交点最多有1个;
③f(x)=x2﹣2x+1与g(t)=t2﹣2t+1是同一函数;
④若f(x)=|x﹣1|﹣|x|,则f(f( ![]() ))=0.
))=0.
其中正确判断的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于四面体![]() ,有以下命题:
,有以下命题:
(1)若![]() ,则过
,则过![]() 向底面
向底面![]() 作垂线,垂足为底面
作垂线,垂足为底面![]() 的外心;
的外心;
(2)若![]() ,
, ![]() ,则过
,则过![]() 向底面
向底面![]() 作垂线,垂足为底面
作垂线,垂足为底面![]() 的内心;
的内心;
(3)四面体![]() 的四个面中,最多有四个直角三角形;
的四个面中,最多有四个直角三角形;
(4)若四面体![]() 的6条棱长都为1,则它的内切球的表面积为
的6条棱长都为1,则它的内切球的表面积为![]() .
.
其中正确的命题是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+1|+|2x﹣a|.
(1)若f(x)的最小值为2,求a的值;
(2)若f(x)≤|2x﹣4|的解集包含[﹣2,﹣1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在
定义在![]() 上且满足下列两个条件:
上且满足下列两个条件:
①对任意![]() 都有
都有![]() ;
;
②当![]() 时,有
时,有![]() ,
,
(1)求![]() ,并证明函数
,并证明函数![]() 在
在![]() 上是奇函数;
上是奇函数;
(2)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(3)若![]() ,试求函数
,试求函数![]() 的零点.
的零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com