
���� ��1����Ȳ�����{an}�Ĺ���Ϊd����a4+a5=0���ɵ�${a}_{1}=-\frac{7}{2}d$���ֱ����õȲ����е�ǰn���ʽ�ɵã�S5��S3��S2��S6�����ɵó���С��ϵ��
��2����Ȳ�����{an}�Ĺ���Ϊd������������k��ʹak+ak+1=0���ɵ�a1=$\frac{��1-2k��d}{2}$������S2k-m-Sm���ɵó���
��3���ڵȱ�����{bn}�У���{bn}��ǰn��˻�Tn=b1•b2•b3��bn��������������k��ʹbkbk+1=1����Tm=T2k-m��m��N*��m��2k�������õȱ����е�ͨ�ʽ����Ȳ����е�ǰn���ʽ���ɵó���
��� ��1���⣺��Ȳ�����{an}�Ĺ���Ϊd����a4+a5=0��
��2a1+7d=0�����${a}_{1}=-\frac{7}{2}d$��
��S5=5a1+$\frac{5��4}{2}d$=-$\frac{15}{2}$d��
S3=$3{a}_{1}+\frac{3��2}{2}d$=-$\frac{15}{2}$d��
��S5=S3��
S2=$2{a}_{1}+\frac{2��1}{2}d$=-6d��
S6=6a1+$\frac{6��5}{2}d$=-6d��
��d��0ʱ��S2��S6��
��d��0ʱ��S2��S6��
��2��֤������Ȳ�����{an}�Ĺ���Ϊd��
�ߴ���������k��ʹak+ak+1=0��
��2a1+��2k-1��d=0��
��a1=$\frac{��1-2k��d}{2}$��
��S2k-m-Sm=��2k-m��a1+$\frac{��2k-m����2k-m-1��}{2}$d-[$m{a}_{1}+\frac{m��m-1��}{2}d$]
=��2k-2m����$\frac{��1-2k��d}{2}$+[2k2-k��2m+1��+m]d
=[-2k2+��2m+1��k-m]d+[2k2-k��2m+1��+m]d
=0��
��3���ڵȱ�����{bn}�У���{bn}��ǰn��˻�Tn=b1•b2•b3��bn��������������k��ʹbkbk+1=1����Tm=T2k-m��m��N*��m��2k����
֤������bkbk+1=1����${b}_{1}^{2}{q}^{2k-1}$=1��
��$\frac{{T}_{2k-m}}{{T}_{m}}$=$\frac{{b}_{1}{b}_{2}•��•{b}_{2k-m}}{{b}_{1}{b}_{2}•��•{b}_{m}}$=$\frac{{b}_{1}^{2k-m}{q}^{1+2+��+��2k-m-1��}}{{b}_{1}^{m}{q}^{1+2+��+��m-1��}}$=$\frac{{b}_{1}^{2k-m}{q}^{��2k-m����2k-m-1��}}{{b}_{1}^{m}{q}^{\frac{m��m-1��}{2}}}$=$��{b}_{1}^{2}{q}^{2k-1}��^{k-m}$=1��
��Tm=T2k-m��m��N*��m��2k����
���� ���⿼���˵��ƹ�ϵ��Ӧ�á��Ȳ����е�ͨ�ʽ����ǰn���ʽ��������������������������������е��⣮


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
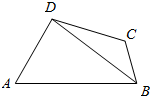 ��ͼ�����ı���ABCD�У�AB=8��BC=3��CD=5����A=$\frac{��}{3}$��cos��ADB=$\frac{1}{7}$��
��ͼ�����ı���ABCD�У�AB=8��BC=3��CD=5����A=$\frac{��}{3}$��cos��ADB=$\frac{1}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com