
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性求得函数f(x)的最小正周期.
(2)由条件利用正弦函数的定义域和值域,求得m的值,从而求得f(x)在区间[0,$\frac{π}{2}$]上的最小值.
解答 解:(1)函数f(x)=2cosx($\sqrt{3}$sinx+cosx)+m
=$\sqrt{3}$sin2x+cos2x+1+m=2sin(2x+$\frac{π}{6}$)+1+m,
故函数f(x)的最小正周期为π.
(2)在区间[0,$\frac{π}{2}$]上,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
故当2x+$\frac{π}{6}$=$\frac{π}{2}$时,f(x)取得最大值为2+1+m=6,∴m=3.
故当2x+$\frac{π}{6}$=$\frac{7π}{6}$时,f(x)取得最小值为-1+1+m=3.
点评 本题主要考查三角恒等变换,正弦函数的周期性、正弦函数的定义域和值域,属于基础题.


科目:高中数学 来源: 题型:填空题
 如图,正方形边长是2,函数y=$\frac{1}{2x}$与正方形交于两点,向正方形内投飞镖,则飞镖落在阴影部分内的概率是$\frac{7-3ln2}{8}$.
如图,正方形边长是2,函数y=$\frac{1}{2x}$与正方形交于两点,向正方形内投飞镖,则飞镖落在阴影部分内的概率是$\frac{7-3ln2}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
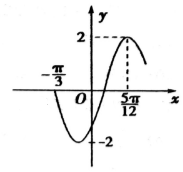 函数f(x)=Asin(ωx+φ),x∈R,(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ),x∈R,(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
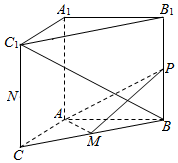 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,CAB=90°,AB=AC=2,AA1=$\sqrt{3}$,M为BC的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,CAB=90°,AB=AC=2,AA1=$\sqrt{3}$,M为BC的中点,P为侧棱BB1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{6}$升 | B. | $\frac{7}{2}$升 | C. | $\frac{113}{66}$升 | D. | $\frac{109}{33}$升 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com