
【题目】已知cos(π+α)= ![]() ,且
,且 ![]() <α<π.
<α<π.
(Ⅰ)求5sin(α+π)﹣4tan(3π﹣α)的值
(Ⅱ)若0<β< ![]() ,cos(β﹣α)=
,cos(β﹣α)= ![]() ,求sin(
,求sin( ![]() +2β)的值.
+2β)的值.
【答案】解:(Ⅰ)∵cos(π+α)= ![]() =﹣cosα,且
=﹣cosα,且 ![]() <α<π,
<α<π,
∴cosα=﹣ ![]() ,sinα=
,sinα= ![]() =
= ![]() ,tanα=﹣
,tanα=﹣ ![]() ,
,
∴5sin(α+π)﹣4tan(3π﹣α)=﹣5sinα+4tanα=(﹣5)× ![]() +4×(﹣
+4×(﹣ ![]() )=﹣6.
)=﹣6.
(Ⅱ)∵0<β< ![]() ,cos(β﹣α)=
,cos(β﹣α)= ![]() ,
,
∴﹣π<β﹣α<0,可得:sin(β﹣α)=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴cosβ=cos[(β﹣α)+α]=cos(β﹣α)cosα﹣sin(β﹣α)sinα= ![]() ×(﹣
×(﹣ ![]() )﹣(﹣
)﹣(﹣ ![]() )×
)× ![]() =
= ![]()
∴sin( ![]() +2β)=cos2β=2cos2β﹣1=﹣
+2β)=cos2β=2cos2β﹣1=﹣ ![]() .
.
【解析】(1)由已知利用诱导公式,通宵三角函数的基本关系式,可得cosα,sinα,tanα,由诱导公式化简即可计算出结果,(2)利用角的范围及同角三角函数基本关系式可得sin(β-α)的值,利用两角和的余弦函数公式可得cosβ=cos[(β﹣α)+α]的值,进而利用诱导公式,二倍角的余弦函数公式即可计算得解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行.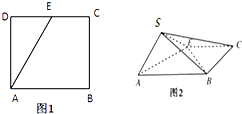
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )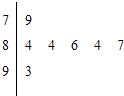
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果画出如图所示的频率分布直方图,其中工资收入分组区间是[10,15),[15,20),[20,25),[25,30)[30,35),[35,40](单位:百元)
(Ⅰ)为了了解工薪阶层对工资收入的满意程度,要用分层抽样的方法从调查的1000人中抽取100人做电话询问,求月工资收入在[30,35)内应抽取的人数;
(Ⅱ)根据频率分布直方图估计这1000人的平均月工资为多少元.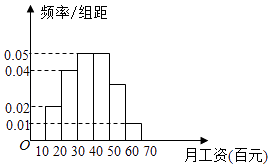
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①mn=nm类比得到ab=ba;
②(m+n)t=mt+nt类比得到(a+b)c=ac+bc;
③(mn)t=m(nt) 类比得到(ab)c=a(bc);
④t≠0,mt=rtm=r类比得到p≠0,ap=bpa=b;
⑤|mn|=|m||n|类比得到|ab|=|a||b|;
⑥ ![]() =
= ![]() 类比得到
类比得到 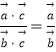 .
.
以上式子中,类比得到的结论正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(Ⅰ)将V表示成r的函数V(r),并求该函数的定义域;
(Ⅱ)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.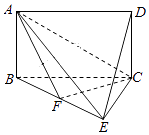
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上,若DE∥平面ACF,DC=CE= ![]() BC=3,求三棱锥A﹣BCF的体积.
BC=3,求三棱锥A﹣BCF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 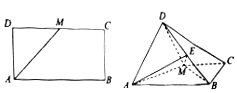
(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com