|
|
|
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为p=2cosθ, ∈[0, ∈[0,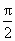 ]. ].
(Ⅰ)求C的参数方程;
(Ⅱ)设点D在C上,C在D处的切线与直线l:y=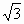 x+2垂直,根据(I)中你得到的参数方程,确定D的坐标. x+2垂直,根据(I)中你得到的参数方程,确定D的坐标.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.
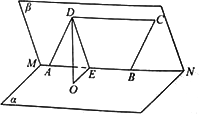
(1)证明:AB⊥平面ODE;
(2)求异面直线BC与OD所成角的余弦值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
某项研究表明:在考虑行车安全的情况下,某路段车流量F(单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v(假设车辆以相同速度v行驶,单位:米/秒)、平均车长l(单位:米)的值有关,其公式为F=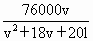 . .
(Ⅰ)如果不限定车型,l=6.05,则最大车流量为________辆/小时;
(Ⅱ)如果限定车型,l=5,则最大车流量比(Ⅰ)中的最大车流量增加________辆/小时.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是
|
| [ ] |
A. |
(-∞,-2]
|
B. |
(-∞,-1]
|
C. |
[2,+∞)
|
D. |
[1,+∞)
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,四凌锥p-ABCD中,底面ABCD为矩形,PA上面ABCD,E为PD的点.
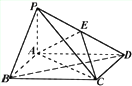
(Ⅰ)证明:PP∥平面AEC;
(Ⅱ)设置AP=1,AD=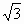 ,三凌P-ABD的体积V= ,三凌P-ABD的体积V=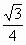 ,求A到平面PBC的距离. ,求A到平面PBC的距离.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
钝角三角形ABC的面积是 ,AB=1, ,AB=1,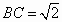 ,则AC= ,则AC=
|
| [ ] |
A. |
5
|
B. |
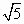
|
C. |
2
|
D. |
1
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为
|
| [ ] |
A. |
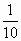
|
B. |
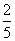
|
C. |
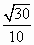
|
D. |
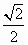
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若向量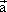 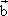 满足:| 满足:|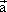 |=1,( |=1,(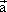 + +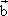 )⊥ )⊥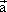 (2 (2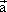 + +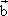 )⊥ )⊥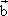 ,则| ,则|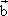 |= |=
|
| [ ] |
A. |
2
|
B. |
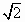
|
C. |
1
|
D. |
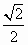
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知复数z满足(3+4i)z=25,则z=
|
| [ ] |
A. |
3-4i
|
B. |
3+4i
|
C. |
-3-4i
|
D. |
-3+4i
|
|
|
查看答案和解析>>
