
| 日需求量n | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数(天) | 10 | 20 | 20 | 14 | 13 | 13 | 10 |
分析 (1)根每个制作成本为50元,当天以每个100元售出,若当天白天售不出,则当晚已30元/个价格作普通蛋糕低价售出,即可建立分段函数;
(2)(i)这100天的日利润的平均数,利用100天的销售量除以100即可得到结论;
(ii)当天的利润不少于900元,当且仅当日需求量不少于19枝,故可求当天的利润不少于900元的概率.
解答 解:(1)当日需求量n≥20时,利润y=1000;当日需求量n<20时,利润y=50n-20(20-n)=70n-400;(4分)
∴利润y关于当天需求量n的函数解析式y=$\left\{\begin{array}{l}{70n-400,n<20}\\{1000,n≥20}\end{array}\right.$(n∈N*)(6分)
(2)(i)这100天的日利润的平均数为$\frac{790×10+860×20+930×20+1000×50}{100}$=937;(9分)
(ii)当天的利润不少于900元,当且仅当日需求量不少于19枝,故当天的利润不少于900元的概率为P=0.2+0.14+0.13+0.13+0.1=0.7.(12分)
点评 本题考查函数解析式的确定,考查概率知识,考查利用数学知识解决实际问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
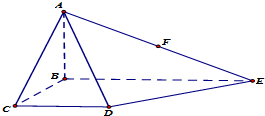 如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.
如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com