
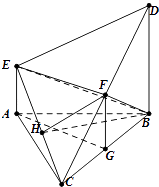
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
(Ⅰ)若F是线段CD的中点,证明:EF⊥面DBC;
(Ⅱ)求二面角D﹣EC﹣B的平面角的余弦值.
【答案】证明:(Ⅰ)取BC的中点G,连接FG,AG,
∵AG⊥BC,AG⊥BD,BD∩BC=B,
∴AG⊥面DBC,
又∵AE∥BD∥FG,AE=FG,
∴AGFE为平行四边形,
∴EF∥AG,∴EF⊥面DBC.
解:(Ⅱ)连接BF,过F在面DEC内作EC的垂线,垂足为H
连接HB.∵EF⊥面DBC,∴BF⊥EF,
又∵BC=BD,∴BF⊥CD,∴BF⊥面EDC,
∴∠FHB为二面角D﹣EC﹣B的平面角,
在△DEC中,∵ ![]() ,∴
,∴ ![]() ,
,
在直角△BFH中, ![]() ,
, ![]() ,
, ![]() ,
,
∴cos∠FHB= ![]() =
= ![]() .
.
∴二面角D﹣EC﹣B的平面角的余弦值为 ![]() .
.
【解析】(Ⅰ)取BC的中点G,连接FG,AG,推导出AG⊥面DBC,AGFE为平行四边形,由此能证明EF⊥面DBC.(Ⅱ)连接BF,过F在面DEC内作EC的垂线,垂足为H,连接HB,则∠FHB为二面角D﹣EC﹣B的平面角,由此能求出二面角D﹣EC﹣B的平面角的余弦值.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC中,a,b,c为角A,B,C所对的边,且![]() .
.
(1)求cosA的值;
(2)若△ABC的面积为![]() ,并且边AB上的中线CM的长为
,并且边AB上的中线CM的长为![]() ,求b,c的长.
,求b,c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设![]() 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意(x1 , y1)∈M,存在(x2 , y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={ ![]() };
};
②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};
④M={(x,y)|y=ex﹣2}.
其中是“垂直对点集”的序号是( )
A.①②
B.②③
C.①④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一则“清华大学要求从 2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.其实,已有不少高校将游泳列为必修内容.
某中学拟在高一-下学期开设游泳选修课,为了了解高--学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1).请将上述列联表![]() 补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
(2)已知在被调查的学生中有6名来自高一(1) 班,其中4名喜欢游泳,现从这6名学生中随机抽取2人,求恰有1人喜欢游泳的概率.
附:![]()
| 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 /td> | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系中椭圆C的方程为ρ2= ![]() ,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(1)求该椭圆的直角标方程,若椭圆上任一点坐标为P(x,y),求x+ ![]() y的取值范围;
y的取值范围;
(2)若椭圆的两条弦AB,CD交于点Q,且直线AB与CD的倾斜角互补,求证:|QA||QB|=|QC||QD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为( )
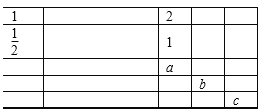
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当∠AOB为锐角时,求k的取值范围;
,当∠AOB为锐角时,求k的取值范围;
(3)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点。
是否过定点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com