
分析 (1)根据韦达定理求出x1+x2,x1•x2的值,证明即可;
(2)由△>0,求出a的范围,从而证出结论;
(3)求出x2=-$\frac{{x}_{1}}{1{+x}_{1}}$,由$\frac{1}{10}$≤$\frac{{x}_{1}}{{x}_{2}}$≤10,得到$\frac{1}{10}$≤-(1+x1)≤10,求出a的范围即可.
解答 (1)证明:由题意得:
x1+x2=-$\frac{1}{a}$,x1•x2=$\frac{1}{a}$,
∴(1+x1)(1+x2)=x1x2+(x1+x2)+1=1;
(2)证明:由△=1-4a>0,解得:a<$\frac{1}{4}$,
∵(1+x1)(1+x2)=1>0,
而(1+x1)(1+x2)=x1+x2+2=-$\frac{1}{a}$+2<-4+2<0,
∴1+x1<0,1+x2<0,
故x1<-1,x2<-1;
(3)解:x2=-$\frac{{x}_{1}}{1{+x}_{1}}$,|lg$\frac{{x}_{1}}{{x}_{2}}$|≤1,
∵$\frac{1}{10}$≤$\frac{{x}_{1}}{{x}_{2}}$≤10,
∴$\frac{1}{10}$≤-(1+x1)≤10,
∴-11≤x1≤-$\frac{11}{10}$,
a=$\frac{1}{{{x}_{1}x}_{2}}$=-($\frac{1}{{{x}_{1}}^{2}}$+$\frac{1}{{x}_{1}}$)=-${(\frac{1}{{x}_{1}}+\frac{1}{2})}^{2}$+$\frac{1}{4}$,
当$\frac{1}{{x}_{1}}$=-$\frac{1}{2}$时,
a的最大值是$\frac{1}{4}$,
当$\frac{1}{{x}_{1}}$=-$\frac{1}{11}$时,
a的最小值是$\frac{10}{121}$,
故a的范围是[$\frac{10}{121}$,$\frac{1}{4}$].
点评 本题考查了二次函数的性质,考查函数的单调性、最值问题,是一道中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
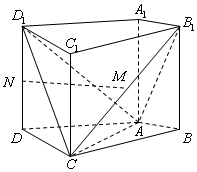 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
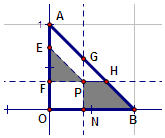 △AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.
△AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com