
【题目】已知![]() 为正的常数,函数
为正的常数,函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设![]() ,求
,求![]() 在区间
在区间![]() 上的最小值.(
上的最小值.(![]() 为自然对数的底数)
为自然对数的底数)
科目:高中数学 来源: 题型:
【题目】为了迎接第二届国际互联网大会,组委会对报名参加服务的![]() 名志愿者进行互联网知识测试,从这
名志愿者进行互联网知识测试,从这![]() 名志愿者中采用随机抽样的方法抽取
名志愿者中采用随机抽样的方法抽取![]() 人,所得成绩如下:
人,所得成绩如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)作出抽取的![]() 人的测试成绩的茎叶图,以频率为概率,估计这
人的测试成绩的茎叶图,以频率为概率,估计这![]() 志愿者中成绩不低于
志愿者中成绩不低于![]() 分的人数;
分的人数;
(2)从抽取的成绩不低于![]() 分的志愿者中,随机选
分的志愿者中,随机选![]() 名参加某项活动,求选取的
名参加某项活动,求选取的![]() 人恰有一人成绩不低于
人恰有一人成绩不低于![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某图书公司有一款图书的历史收益率(收益率=利润÷每本收入)的频率分布直方图如图所示:

(1)试估计平均收益率;(用区间中点值代替每一组的数值)
(2)根据经验,若每本图书的收入在20元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:

据此计算出的回归方程为![]()
①求参数![]() 的估计值;
的估计值;
②若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,
的线性关系, ![]() 取何值时,此产品获得最大收益,并求出该最大收益.
取何值时,此产品获得最大收益,并求出该最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A-BCD中,AB=a,AC=AD=b,BC=CD=DB=c(a>0,b>0,c>0)该三棱锥的截面EFGH平行于AB、CD,分别交AD、AC、BC、BD于E、F、G、H.
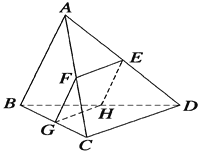
(1)证明:AB⊥CD;
(2)求截面四边形EFGH面积的最大值,并说明面积取最大值时截面的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圆C2:x2+y2=1.
(1)过定点M(1,-2)作圆C2的切线,求切线的方程;
(2)若圆C1与圆C2相交,求m的取值范围;
(3)已知点P(2,0),圆C1上一点A,圆C2上一点B,求|![]() |的最小值的取值范围.
|的最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下五个关于圆锥曲线的命题中:
①平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹为![]() ;
;
②点P是抛物线![]() 上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则
上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则![]() 的最小值是6;
的最小值是6;
③平面内到两定点距离之比等于常数![]() 的点的轨迹是圆;
的点的轨迹是圆;
④若过点C(1,1)的直线![]() 交椭圆
交椭圆![]() 于不同的两点A,B,且C是AB的中点,则直线
于不同的两点A,B,且C是AB的中点,则直线![]() 的方程是
的方程是![]() .
.
⑤已知P为抛物线![]() 上一个动点,Q为圆
上一个动点,Q为圆![]() 上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是
上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是![]()
其中真命题的序号是______.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左顶点到直线
,左顶点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线![]() 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面半径为![]() ,母线长为
,母线长为![]() 的圆柱的轴截面是四边形
的圆柱的轴截面是四边形![]() ,线段
,线段![]() 上的两动点
上的两动点![]() ,
, ![]() 满足
满足![]() .点
.点![]() 在底面圆
在底面圆![]() 上,且
上,且![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)四棱锥![]() 的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com