
【题目】已知定理:“实数m,n为常数,若函数h(x)满足h(m+x)+h(m﹣x)=2n,则函数y=h(x)的图象关于点(m,n)成中心对称”.
(1)已知函数f(x)= ![]() 的图象关于点(1,b)成中心对称,求实数b的值;
的图象关于点(1,b)成中心对称,求实数b的值;
(2)已知函数g(x)满足g(2+x)+g(﹣x)=4,当x∈[0,2]时,都有g(x)≤3成立,且当x∈[0,1]时,g(x)=2k(x﹣1)+1 , 求实数k的取值范围.
【答案】
(1)解:函数f(x)= ![]() 的图象关于点(1,b)成中心对称,
的图象关于点(1,b)成中心对称,
可得f(1+x)+f(1﹣x)=2b,
即有 ![]() +
+ ![]() =4=2b,
=4=2b,
解得b=2;
(2)解:由g(2+x)+g(﹣x)=4可得g(x)的图象关于点(1,2)对称,
且g(1)=2,
当k=0时,g(x)=2(0≤x≤1),又g(x)关于(1,2)对称,
可得g(x)=2(0≤x≤2),显然g(x)≤3恒成立;
当k>0时,g(x)=2k(x﹣1)+1在[0,1]递增,又g(x)关于点(1,2)对称,
可得g(x)在[0,2]递增,g(x)≤3,只需g(x)max=g(2)≤3,
又g(2)+g(0)=4,则g(0)≥1即21﹣k≥1,
即有0≤k≤1;
当k<0时,g(x)=2k(x﹣1)+1在[0,1]递减,又g(x)关于(1,2)对称,
可得g(x)在[0,2]递减,要使g(x)≤3,只需g(x)max=g(0)≤3,
即21﹣k≤3,解得1﹣log23≤k<0.
综上可得,1﹣log23≤k≤1
【解析】(1)由对称性可得f(1+x)+f(1﹣x)=2b,化简整理,即可得到b=2;(2)由g(2+x)+g(﹣x)=4可得g(x)的图象关于点(1,2)对称,且g(1)=2,对k讨论,当k=0,k>0,k<0,结合对称性和单调性,要使g(x)≤3,只需g(x)max≤3,运用单调性求得最大值,解不等式即可得到所求范围.


科目:高中数学 来源: 题型:
【题目】已知 ![]() ,函数 f(x)=x2(x-a) ,若f'(1)=1 .
,函数 f(x)=x2(x-a) ,若f'(1)=1 .
(1)求 a 的值并求曲线 y=f(x) 在点(1,f(1)) 处的切线方程y=g(x) ;
(2)设h(x)=f'(x)+g(x) ,求 h(x) 在 [0,1] 上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣6x﹣4y+4=0,点P(6,0).
(1)求过点P且与圆C相切的直线方程l;
(2)若圆M与圆C外切,且与x轴切于点P,求圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( ) 
A.在区间(﹣2,1)上f(x)是增函数
B.在(1,3)上f(x)是减函数
C.在(4,5)上f(x)是增函数
D.当x=4时,f(x)取极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 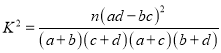 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况,![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)

(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三角A,B,C的对边分别为a,b,c满足(2b﹣c)cosA=acosC.
(1)求A的值;
(2)若a=2,求△ABC面积的最大值;
(3)若a=2,求△ABC周长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com